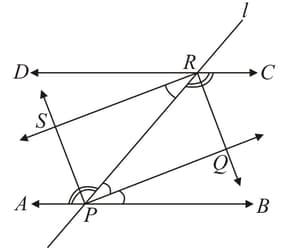
In the adjacent figure, and are two parallel lines which are intersected by transversal at points and respectively. Prove that the bisectors of the interior angles make a rectangle.


Important Questions on Quadrilaterals
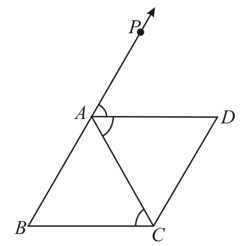
is an isosceles triangle in which , bisects the exterior angle and . Prove that
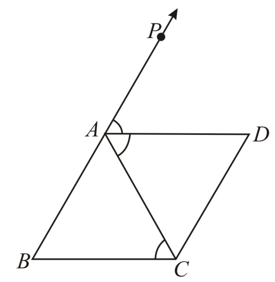
is an isosceles triangle in which , bisects the exterior angle and . Prove that quadrilateral is a parallelogram.
is a parallelogram and is one of its diagonals. and are perpendiculars on from the vertices and respectively. Prove that
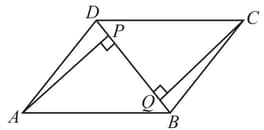
is a parallelogram and is one of its diagonals. and are perpendiculars on from the vertices and respectively. Prove that .
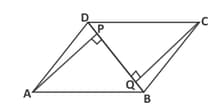
is a rectangle in which diagonal bisects both the angles and . Then prove that is a square.
is a rectangle in which diagonal bisects both the angles and . Then prove that diagonal bisects both angles and .
and are such that and are equal and parallel to and respectively. Prove that and are equal and parallel.
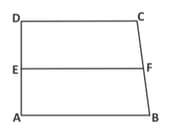
is a trapezium where . is the midpoint of . A line drawn from , parallel to , meets at point . Prove that is the mid point of .