In the construction of orthocentre to the triangle, the following steps are to be followed

• Find the perpendicular from any two vertices to the opposite sides.
• To draw the perpendicular or the altitude, use vertex C as the center and radius equal to the side BC. Draw arcs on the opposite sides AB and AC.
• ?
• Similarly, draw intersecting arcs from points C and E, at G. Join BG.
• CF and BG are altitudes or perpendiculars for the sides AB and AC respectively.
• The intersection point of any two altitudes of a triangle gives the orthocenter.
• Thus, find the point of intersection of the two altitudes.
• At that point, H is referred to as the orthocenter of the triangle.

Consider the following statements:

$1.$The orthocentre of a triangle always lies inside the triangle.

$2.$The centroid of a triangle always lies inside the triangle.

$3.$The orthocentre of a right-angled triangle lies on the triangle.

$4.$The centroid of a right-angled triangle lies on the triangle.

Which of the above statements are correct?

Consider the following statements:

1. The point of intersection of the perpendicular bisectors of the sides of a triangle may lie outside the triangle.

2. The point of intersection of the perpendiculars drawn from the vertices to the opposite sides of a triangle may lie on two sides.

Which of the above statements is/are correct?

Find the in-radius (in cm) of an equilateral triangle whose sides are $6$ cm each.

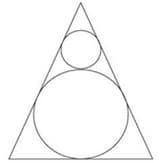
Two circles are placed in an equilateral triangle as shown in the figure. What ratio of the area of the larger circle to that of the equilateral triangle?

Construct $\Delta ABC$ such that $\angle B=100°, BC=6.4, \angle C=50°$ and construct its incircle.