In the figure below, O is the centre of two concentric circles. $∆\mathrm{PQR}$ is an equilateral triangle such that its vertices and sides touch the bigger and smaller circles respectively. The difference between the area of the bigger circle and the smaller circle is 616 cm².

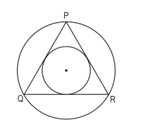
Find the perimeter of $∆\mathrm{PQR}.$

Shown below is a circle with centre M. PQ is a secant and $\angle \mathrm{KML} = \mathrm{\theta }$

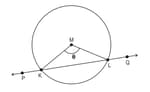
i) Show that, when $\mathrm{\theta }=0°$ PQ becomes a tangent to the circle.

ii) What is the point of contact of the tangent in part i) with the circle?

Shown below is a circle whose centre is unknown.

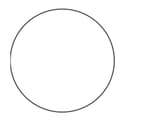
State true or false for the statements below and give valid reasons.

i) The centre of the circle can be found using any 2 tangents.
ii) The centre of the circle can be found using any 2 chords.

Shown below is a $∆\mathrm{PQR}$ inscribed in a semicircle.

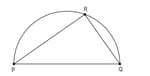
A circle is drawn such that QR is a tangent to it at the point R. How many such circles can be drawn? 

In the figure below, PQ and RQ are tangents to the circle with centre O and radius 6cm

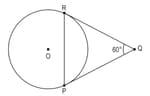
i) Prove that $△\mathrm{PQR}$ is an equilateral triangle.
ii) Find the length of RP. 

A point is 25 cm from the centre of a circle of radius 15 cm. Find the length of the tangent from the point to the circle. 

In the figure below, a circle with centre O is inscribed inside ALMN. A and B are the points of tangency.

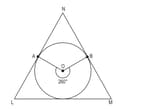
Find $\angle \mathrm{ANB}.$

Shown below is a circle with centre $\mathrm{O}$. VP = 34 cm, PR = 36 cm and RS = 17 cm. U, W, Q and S are the points of tangency.

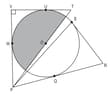
Find the area of the shaded region in terms of $\mathrm{\pi }$. 

Shown below is a circle with centre O and radius 5 units. PM and PN are tangents and the length of chord MN is 6 units.

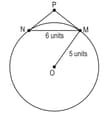
Find the length of (PM + PN). Show your work.