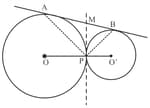
In the figure given below, and are centres of two circles touching each other externally at the point . The common tangent at meets a direct common tangent at . Prove that:


Important Questions on Circle
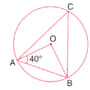
In the adjoining figure, is the centre of the circle. If , then is equal to
In the adjoining figure, is the centre of the circle. If , then is equal to
In the adjoining figure, is the centre of a circle. If the length of chord is equal to the radius of the circle, then is
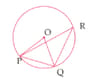
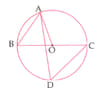
In the adjoining figure, if is the centre of the circle then the value of is
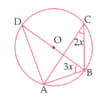
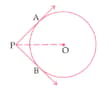
From a point which is at a distance of from the centre of a circle of radius , the pair of tangents and to the circle are drawn. Then the area of the quadrilateral is
In the adjoining figure, and are tangents from to a circle with centre . If , then is
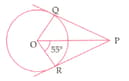
In the adjoining figure, and are tangents from point to a circle with centre . If the radius of the circle is and , then the length is equal to