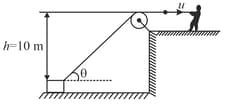
In the figure shown, a person pulls a light string with a constant speed $u=10 \mathrm{m} {\mathrm{s}}^{-1}$. The other end of the string is tied to a very small block which moves on a smooth horizontal surface. The block is initially situated at a distance from the pulley which is very large in comparison to $h$. Find the angle $\mathrm{\theta }$ when the block leaves the surface. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

 

A box having mass $400 \mathrm{kg}$ is to slowly slide through $10 \mathrm{m}$ on a horizontal straight track having friction coefficient $0.2$with the box.

(a) Find the work done by the person pulling the box with a rope at an angle $\mathrm{\theta }$ with the horizontal.

(b) Find the work when the person has chosen a value of $\mathrm{\theta }$ which ensures him the minimum magnitude of the force. $[g=10 \mathrm{m} {\mathrm{s}}^{-2}]$

The pulley (uniform disc) shown in figure has, radius $10 \mathrm{cm}$ and moment of inertia about its axis $I=0.5 \mathrm{kg} {\mathrm{m}}^2$ ($B$ and $A$ both move)

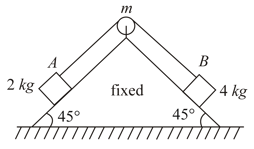
(a) Assuming all the plane surfaces are smooth and there is no slipping between pulley and string, calculate the acceleration of the mass $4 \mathrm{kg}$.

(b) The friction coefficient between the block $A$ and the plane below is $\mu =0.5$ and the plane below the $B$ block is frictionless. Assuming no slipping between pulley and string find acceleration of $4 \mathrm{kg}$ block. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

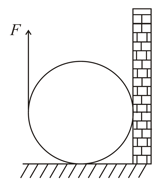
Figure shows a vertical force $F$ that is applied tangentially to a uniform cylinder of weight $W$. The coefficient of static friction between the cylinder and all surfaces is $0.5$. Find in terms of $W$, the maximum force that can be applied without causing the cylinder to rotate.

A wedge of mass $m$and triangular cross section $(AB=BC=CA=2R)$ is moving with a constant velocity-$v\hat{\mathrm{i}}$ towards a sphere of radius $R$ fixed on a smooth horizontal table as shown in the figure. The wedge makes an elastic collision with the fixed sphere and returns along the same path without any rotation. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very short time $∆t$, during which the sphere exerts a constant force $\overrightarrow{F}$ on the wedge. The sphere is always fixed.

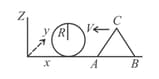
(a) Find the force $\overrightarrow{F}$ and also the normal force $\overrightarrow{N}$ exerted by the table on the wedge during the time $∆t$.

(b) Let $h$denote the perpendicular distance between the centre of mass of the wedge and the line of action of force $\overrightarrow{F}$. Find the magnitude of the torque due to the normal force $\overrightarrow{N}$ about the centre of the wedge, during the time $∆t$.

A particle of mass $m$ is moving in the $x-y$ plane such that its $x$ and $y$ coordinates vary according to the law, $x=a\mathrm{sin\omega }t \text{and} y=a\cos \omega t$ where $a$ and $\mathrm{\omega }$ are positive constants and $t$ is time. Find,

(a) equation of the path. Name the trajectory (path),

(b) whether the particle moves in clockwise or anticlockwise direction,

(c) magnitude of the force on the particle at any time $t$.