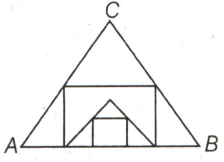
In the following figure, A B C is an equilateral triangle inscribing a square of maximum possible area. Again in this square, there is an equilateral triangle whose side is the same as that of the square. Further, the smaller equilateral triangle inscribes a square of the maximum possible area. What is the area of the innermost square if each side of the outermost triangle be $0.01 \mathrm{m}$ ?

  

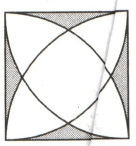
The four vertices of a unit square act as the centers of four quarter-circles. The arcs of these circles intersect each other within the square as depicted below. If the area of the region at the center of the square, which $\left(1\right)$itself looks like a bloated square, is cordoned off by all the four arcs of circles is $\frac{\mathrm{\pi }}{3}-\sqrt{3}+1$, find the area of the shaded region.

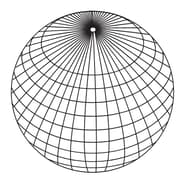
The following diagram depicts the Earth. For the sake of convenience, and simply let us consider that the earth is completely spherical. The earth is completely spherical. The topmost point (N), where all the topmost point (N), where all the great circles meet, is called the North great circles meet, is called the North Pole. South Pole is denoted by the point (S) is exactly opposite the North Pole. All the vertical circles are passing through each pole are called longitudes and all the horizontal circles that are parallel to each other are called latitudes.

Let the center of the earth be denoted by C and the radius of the earth is $6370 \mathrm{km}$. A man has to reach from the North Pole to a point D on the latitude with radius $3185\sqrt{3} \mathrm{km}$ in the Southern hemisphere of the earth. Find the minimum distance along the surface of the earth that he will have to traverse.