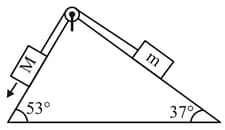
In the given arrangement of a doubly inclined plane two blocks of masses and are placed. The blocks are connected by a light string passing over an ideal pulley as shown. The coefficient of friction between the surface of the plane and the blocks is . The value of , for which will move down with an acceleration of , is : (take and )

Important Questions on Friction
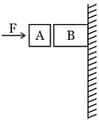
Given in the figure are two blocks and of weight and , respectively. These are being pressed against a wall by a force and kept in equilibrium as shown. If the coefficient of friction between the blocks is and between block and the wall is , the frictional force applied by the wall on block is:
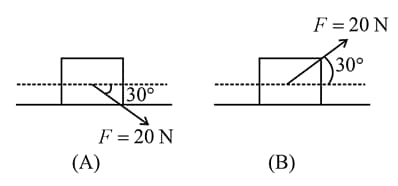
A block of mass is (i) pushed in case and (ii) pulled in case by a force making an angle of with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is The difference between the accelerations of the block, in case and case will be:
A block of mass resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass . The coefficient of kinetic friction between the block and the surface is . Tension in the cord is
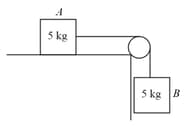
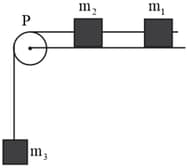
Consider the system shown below.
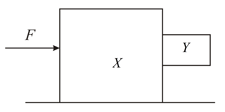
A horizontal force is applied to a block of mass such that the block of mass adjacent to it does not slip downwards under gravity. There is no friction between the horizontal plane and the base of the block . The coefficient of friction between the surfaces of the blocks and is . Take acceleration due to gravity to be . The minimum value of is
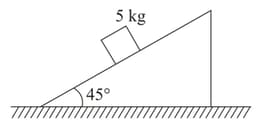
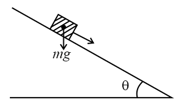
A block of mass is kept against an accelerating wedge with a wedge angle of to the horizontal. The co-efficient of friction between the block and the wedge is . What is the minimum absolute value of the acceleration of the wedge to keep the block steady. Assume