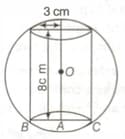
In the given figure, a sphere circumscribes a right cylinder whose height is $8 \mathrm{cm}$ and the radius of the base is $3 \mathrm{cm}$. Find the ratio of the volumes of the sphere and the cylinder.

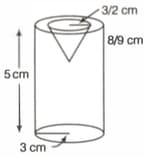
A metallic cylinder has radius $3 \mathrm{cm}$ and height $5 \mathrm{cm}$. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder as shown in the figure and it is completely filled with a lighter metal B. The conical hole has a radius of $\frac{3}{2} \mathrm{cm}$ and its depth is $\frac{8}{9} \mathrm{cm}$. Calculate the ratio of the volume of the metal A to the volume of the metal B. 

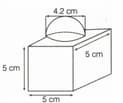
The decorative block as shown in the figure is made of two solids, a cube and a hemisphere. The base of the block is a cube with edge $5 \mathrm{cm}$ and the hemisphere fixed on the top has a diameter of $4.2 \mathrm{cm}$, then find the total surface area of the block and find the total area to be painted.

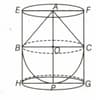
In the given figure, a solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is $2 \mathrm{cm}$ and the diameter of the base is $4 \mathrm{cm}$. If a right circular cylinder circumscribes the solid, then find how much more space it will cover?

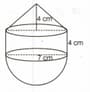
The given figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is $7 \mathrm{cm}$. The height of the cylinder and cone are each of $4 \mathrm{cm}$. Find the volume of the solid.

A conical tent is to accommodate $77$ persons. Each person must have $16 {\mathrm{m}}^3$of air to breathe. Given the radius of the tent as $7 \mathrm{m}$. Find the height of the tent and also its curved surface area.