In the given figure there are twelve rhombi placed in such a way that they form a regular hexagram at the centre and this hexagram is inscribed within a regular hexagon. If the area of the hexagon is$84 \mathrm{sq}. \mathrm{cm},$ find the total area of all the twelve rhombi.

As shown in the given figure, there is a total of seven regular hexagons; six of them are placed around the seventh hexagon. Partially overlapping, and then some rhombi are cut out of the whole arrangement. If the area of the unshaded region represented by the $12$ Rhombi is, $84 \mathrm{sq}. \mathrm{cm},$ Find the area of the shaded region.

If the area of all the shaded equilateral triangles of the largest possible size, as shown along the periphery of the regular hexagon, is $6\sqrt{3} \mathrm{sq} \mathrm{cm},$ then find the total area of the shaded region of the whole figure.

There are seven concentric regular hexagons depicted in the adjacent figure such that they form a six alternating black and white hexagonal rings around a black hexagon. If the area of each hexagonal ring is same and equal to the black hexagon at the centre, find the ratio of the sides of the largest hexagon to that of the smallest hexagon of this arrangement.

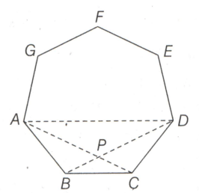
In the following diagram, if the two shorter diagonals $\mathrm{AC}$ and $\mathrm{BD}$ intersect at $\mathrm{P}$ inside the regular heptagon and $\mathrm{AD}$ is one of the longer diagonals, which one of the following is correct?

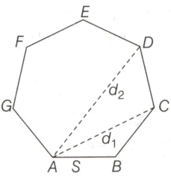
In the following diagram, ${\mathrm{d}}_1, {\mathrm{d}}_2$ are the two distinct diagonals and $\mathrm{s}$ is the side of the regular polygon $\mathrm{ABCDEFG}.$ Find the correct relation among the side and the two diagonals.

Neither it's the longest one nor it's the shortest one of the lengths of the diagonal of an octagon you know is $\mathrm{d}$ and each side of the same octagon is $\mathrm{s},$ find the area of the octagon in terms of the side and the known diagonal of the regular octagon.

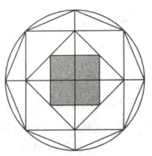
In the given diagram, a regular octagon is inscribed in a circle in which four diagonals are connecting the opposite vertices of the octagon. After that a square is formed by connecting the alternate vertices of the octagon then another square is formed by joining the mid-points of the first square and then finally another square is formed by joining the mid-points of the previous square. This square is shown as the shaded region. If the area of the shaded region is $1$ sq. cm, find the difference between the area of the circle and area of the octagon.

In the given figure a quadrilateral is formed by joining the alternate vertices of a regular octagon. If the area of the octagon be $2(\sqrt{2}-1) \mathrm{sq} \mathrm{cm},$ find the area of the square.