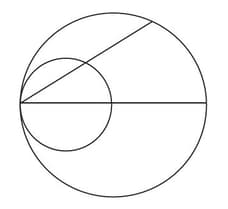
In the picture, a circle is drawn with a line as diameter and a smaller circle with half the line as diameter. Prove that any chord of the longer circle through the point where the circles meet is bisected by the small circle.


Important Questions on Circles
Use a calculator to determine up to two decimal places, the perimeter and the area of the circle in the picture.
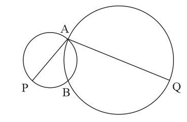
The two circles in the picture cross each other at and . The points and are the other ends of the diameters through . Prove that lie on a line.
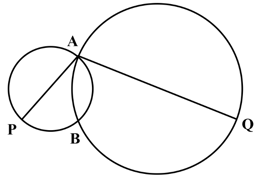
The two circles in the picture cross each other at and . The points and are the other ends of the diameters through . Prove that is parallel to the line joining the centres of the circles and is twice as long as this line.
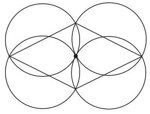
Prove that all four circles drawn with the sides of a rhombus as diameters pass through a common point.
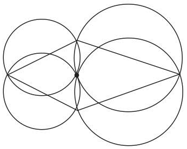
Prove that this is true for any quadrilateral with adjacent sides equal, as in the picture.
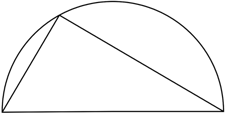
A triangle is drawn by joining a point on a semicircle to the ends of the diameter. Then semicircles are drawn with the other two sides as diameter. Prove that the sum of the areas of the blue and red crescents in the second picture is equal to the area of the triangle.
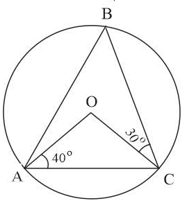
In the picture given below, is the centre of the circle and are points on it. Calculate all angles of and .
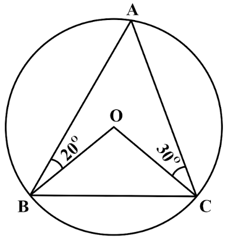
In the picture given below, is the centre of the circle and are points on it. Calculate all angles of and .