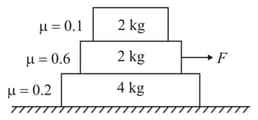
In the situation shown in figure, for what value of minimum horizontal force $F$ (in Newton), sliding between middle and lower block will start ? (Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

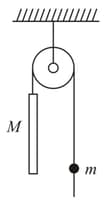
In the arrangement shown in figure, the mass of the rod $M$ exceeds the mass $m$ of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley, mass of the string and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if $t$ seconds after the beginning of motion the ball got opposite the upper end of the rod. The rod length equals $l$.

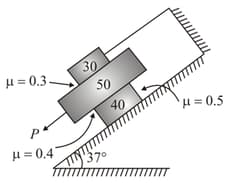
The three flat blocks as shown in the figure are positioned on the $37°$ incline and a force $P$ parallel to the inclined plane is applied to the middle block. The upper block is prevented from moving by a wire which attaches it to the fixed support. The masses of three blocks in $\mathrm{kg}$ and coefficient of static friction for each of the three pairs of contact surfaces are shown in the figure. Determine the maximum value which force $P$ may have before slipping take place anywhere $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$.

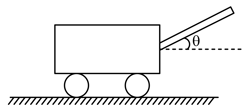
A cart of total mass$\mathit{ }{M}_0$is at rest on a rough horizontal road. It ejects bullets at rate of $\mathrm{\lambda } \mathrm{kg} {\mathrm{s}}^{-1}$ at an angle $\mathrm{\theta }$ with the horizontal and at velocity $u$(constant) relative to the cart. The coefficient of friction between the cart and the ground is $\mathrm{\mu }$. Find the velocity of the cart in terms of time $t$. The cart moves with sliding.

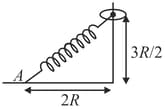
A ring of mass $m$ can slide along a fixed rough vertical rod as shown in the figure. The ring is connected by a spring of spring constant $k=\frac{4mg}{R}$ where $2R$ is the natural length of spring. The other end of the spring is fixed to the ground at a point $A$ at a horizontal distance of $2R$ from the base of the rod. If the ring is released from a height of $3R/2$ and it reaches the ground with a speed $\sqrt{3gR}$, find a co-efficient of friction between the rod and ring.

A uniform cube of side $a$and mass $m$ rests on a rough horizontal table. A horizontal force $F$ is applied normal to one of the faces at a point directly above the centre of the face at a height $\frac{3a}{4}$ above the base. (i) What is the minimum value of $F$ for which the cube begins to tip about an edge?

(ii) What is the minimum value of ${\mu }_{\mathrm{s}}$ so that toppling occurs.

(iii) If $\mu ={\mu }_{\min }$, find minimum force for topping.

(iv) Minimum ${\mu }_{\mathrm{s}}$ so that $F_{\min }$(as in part-(i)) can cause toppling.