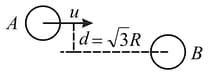In which of the following system(s) linear momentum cannot be conserved during collision along horizontal line (parallel to base)?

A disc moving on a frictionless horizontal table collide elastically with another identical disc as shown. The directions of motion of the two discs make angle $\theta$ and $\varphi$ with the initial line of motion as shown. Then:

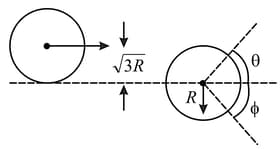
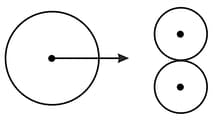
Two equal discs are in contact on a table. A third disc of same mass but of double radius strikes them symmetrically and remains at rest after impact. Find the coefficient of restitution.

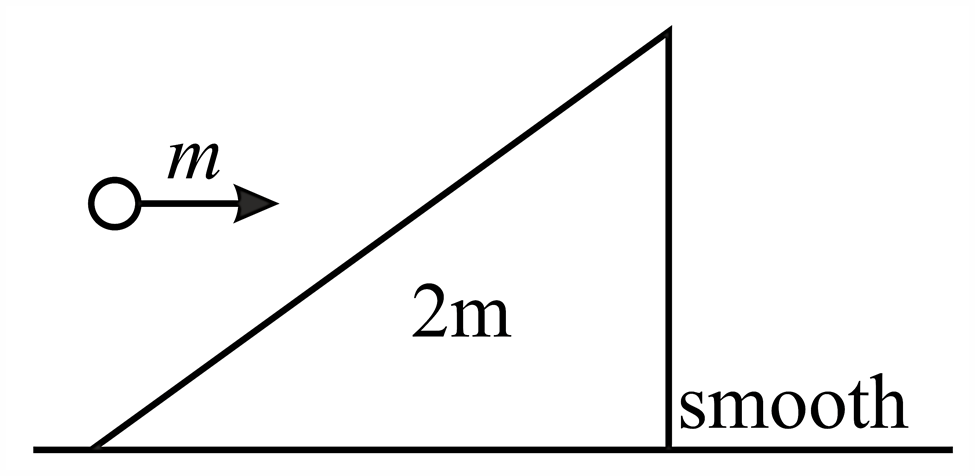
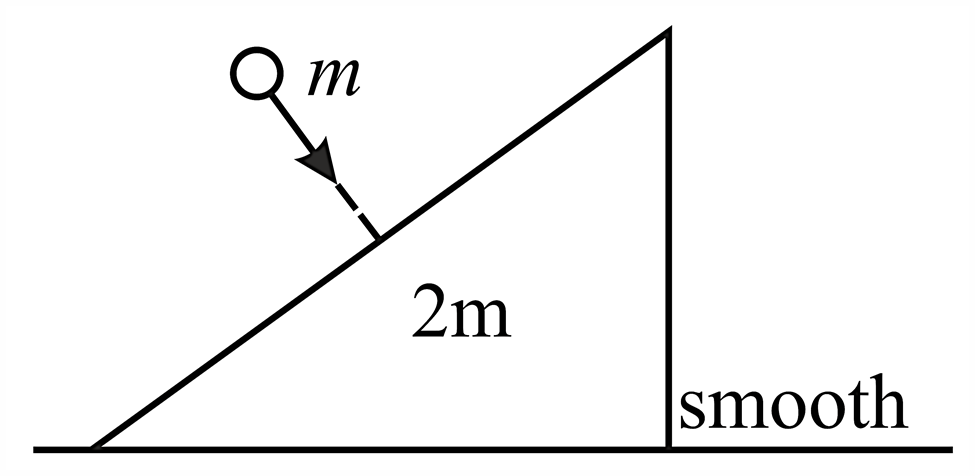
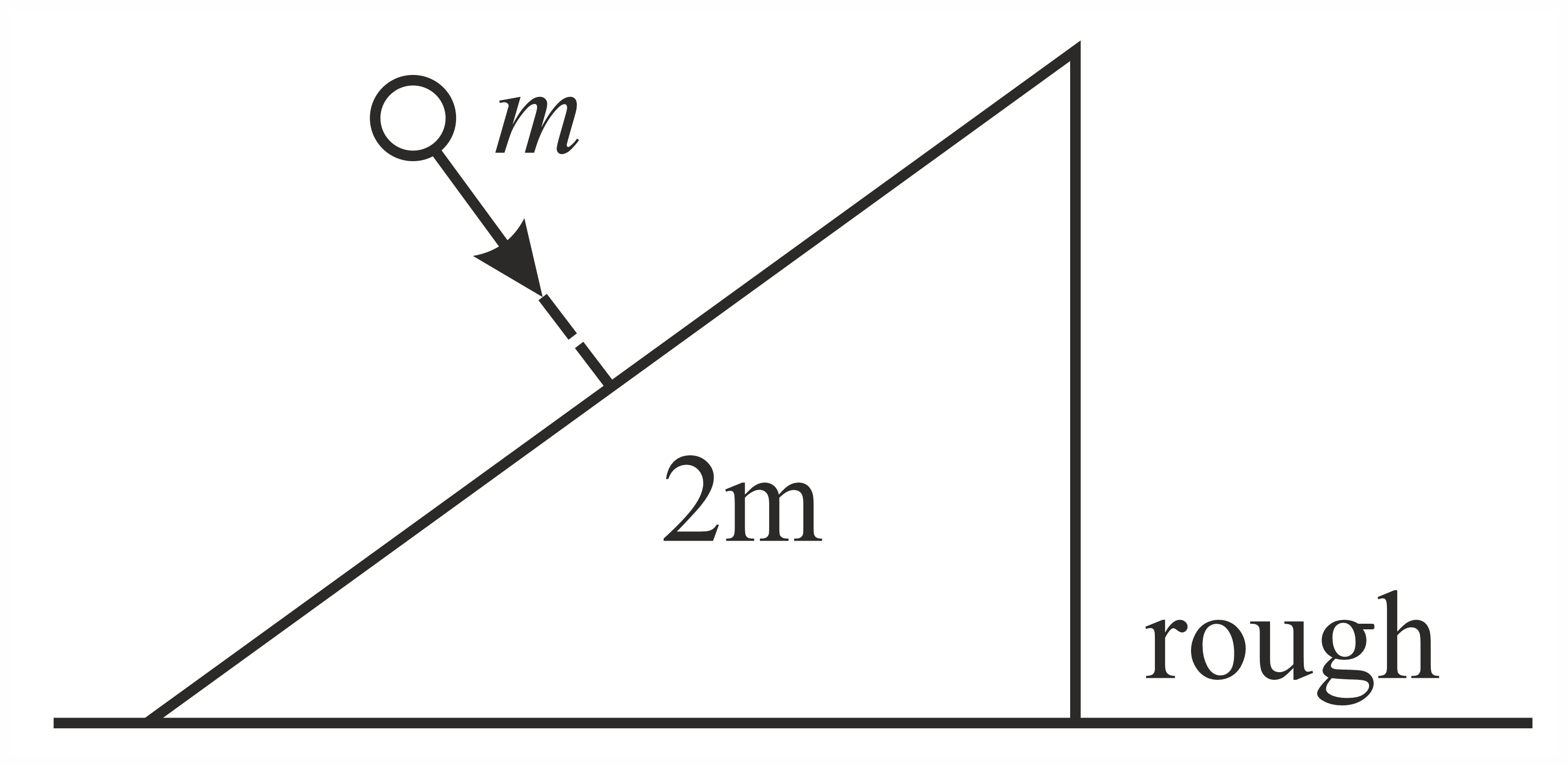
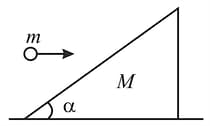
A wedge (free to move) of mass ' $M$ ' has one face making an angle $\alpha$ with horizontal and is resting on a smooth rigid

floor. A particle of mass ' $m$ ' hits the inclined face of the wedge with a horizontal velocity $v_0.$ It is observed that the particle rebounds in vertical direction after impact. Neglect friction between particle and the wedge and take $M=2 \mathrm{m},$ $v_0=10 \mathrm{m} {\mathrm{s}}^{-1}, \tan \alpha =2, g=10 \mathrm{m} {\mathrm{s}}^{-2}.$ Determine the coefficient of restitution for the impact.

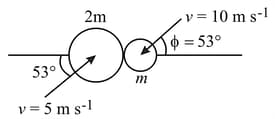
Two smooth spheres made of identical material having masses ' $m$ ' and ' $2m$ ' undergoes an oblique impact as shown in figure. The initial velocities of the masses are also shown. The impact force is along the line joining their centres. The coefficient of restitution is $5/9 .$ Calculate the velocities of the masses after the impact.

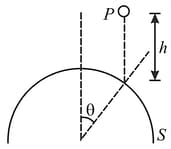
A hemisphere $\text{'}S\text{'}$ and a particle $\text{'}P\text{'}$ are of same mass 'm'. $P$ is dropped from a height ' $h$ '. A hemisphere $\text{'}S\text{'}$ is kept on a smooth horizontal surface. The particle $\text{'}P\text{'}$ collides elastically with hemisphere at the point shown in the figure. If $\theta =45°$ and after collision the velocity of the particle becomes horizontal. Find the velocities of hemisphere ' $S$ ' and particle ' $P$ ' after collision. 

Disc $A$ of mass $m$ collides with stationary disc $B$ of mass $2m$ as shown in figure. Find the value of coefficient of restitution for which the two discs move in perpendicular direction after collision.

A mass ${\mathrm{m}}_1$ with initial speed $v_0$ in the positive $x$ -direction collides with a mass ${\mathrm{m}}_2=2{\mathrm{m}}_1$ which is initially at rest at the origin, as shown in figure. After the collision ${\mathrm{m}}_1$ moves off with speed ${\mathrm{v}}_1=\frac{{\mathrm{v}}_{\circ }}{2}$ in the negative $y$ -direction, and ${\mathrm{m}}_2$ moves off with speed $v_2$ at angle $\theta .$

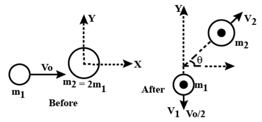
(a) Find the velocity (magnitude and direction) of the centre of mass before the collision, as well as its velocity after the collision.
(b) Find ${\mathrm{v}}_2$ in terms of ${\mathrm{v}}_{\circ }.$

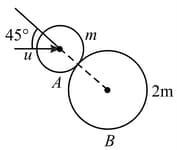
A smooth ball ' $A$ 'travels towards another identical ball ' $B$ with a velocity $u.$ Ball $B$ is at rest and the impact parameter $d$ is equal to $\sqrt{3}R$ where $R$ is radius of each ball. Due to impact the direction of motion of ball $A$ changes by $30°.$ Find the velocities of the balls ' $A$ ' and ' $B$ 'after collision. It is given that collision is elastic.