Kepler's three laws of planetary motion describe how planetary bodies orbit the .
Important Questions on Gravitation
A planet is revolving around the sun in which of the following is correct statement?
India's Mangalyan was sent to the Mars by launching it into a transfer orbit EOM around the sun. It leaves the earth at and meets Mars at . If the semi-major axis of Earth's orbit is , that of Mar's orbit , taking Kepler's laws, give the estimate of time for Mangalyan to reach Mars from Earth.
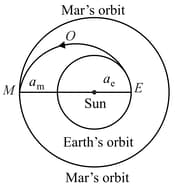
(Assume , where and are gravitational constant and mass of earth and )
A star mass (equal to the solar mass) with a planet (much smaller than the star) revolves around the star in a circular orbit. The velocity of the star with respect to the centre of mass of star-planet system is shown below:
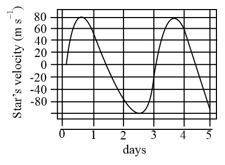
The radius of the planet's orbit is closest to ()
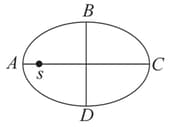
A planet revolving in elliptical orbit has :
A. a constant velocity of revolution.
B. has the least velocity when it is nearest to the sun.
C. its areal velocity is directly proportional to its velocity.
D. areal velocity is inversely proportional to its velocity.
E. to follow a trajectory such that the areal velocity is constant.
Choose the correct answer from the options given below:
Assume that the earth moves around the sun in a circular orbit of radius and there exists a planet that also moves around the sun in a circular orbit with an angular speed twice as large as that of the earth. The radius of the orbit of the planet is,
Assume radius of orbit of planet earth to be .
A planet revolves in an elliptical orbit around the sun. The semi-major and semi-minor axes are and . Then, the square of time period is directly proportional to-

