EASY

Earn 100

Let $(3, 4, - 1) a n d (- 1, 2, 3)$ are the end points of a diameter of sphere. Then the radius of the sphere is equal to

50% studentsanswered this correctly

Important Questions on Three Dimensional Geometry

HARD

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

Three lines

L_{1} : \vec{r} = λ \hat{i}, λ \in R,

L_{2} : \vec{r} = \hat{k} + μ \hat{j}, μ \in R

and

L_{3} : \vec{r} = \hat{i} + \hat{j} + ν \hat{k}, ν \in R

are given. For which point(s)

Q

and

L_{2}

can we find a point

P

L_{1}

and a point

R

L_{3}

so that

P, Q

and

R

are collinear?

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

∆ A B C

has vertices at

A \equiv (2, 3, 5), B \equiv (- 1, 3, 2)

and

C \equiv (λ, 5, μ) .

If the median through

A

is equally inclined to the axes, then the values of

λ

and

μ

respectively are

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

Let

A B C

be a triangle whose circumcentre is at

P

. If the position vectors

A, B, C

and

P

are

\vec{a}, \vec{b}, \vec{c}

and

\frac{\vec{a} + \vec{b} + \vec{c}}{4}

respectively, then the position vector of the orthocentre of this triangle, is :

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

If $Q (0, - 1, - 3)$ is the image of the point $P$ in the plane $3 x - y + 4 z = 2$ and $R$ is the point $(3, - 1, - 2)$ , then the area (in sq. units) of $Δ P Q R$ is

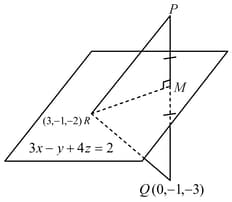
Question Image

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

The radius of the circle formed when the sphere

x^{2} + y^{2} + z^{2} = 49

is cut by the plane

2 x + 3 y - z - 5 \sqrt{14} = 0

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

Let

A (3, 0, - 1), B (2, 10, 6)

and

C (1, 2, 1)

be the vertices of a triangle and

M

be the mid-point of

A C

. If

G

divides

B M

in the ratio,

2 : 1

, then

c o s (∠ G O A)

(

O

being the origin) is equal to

HARD

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

If a variable plane, at a distance of

3

units from the origin, intersects the coordinate axes at

A, B & C

, then the locus of the centroid of

Δ A B C

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

In a triangle

A B C,

if the mid points of sides

A B, B C, C A

are

(3, 0, 0), (0, 4, 0), (0, 0, 5)

, respectively, then

A B^{2} + B C^{2} + C A^{2} =

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

A tetrahedron has vertices

P (1, 2, 1), Q (2, 1, 3), R (- 1, 1, 2)

and

O (0, 0, 0)

. The angle between the faces

O P Q

and

P Q R

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

The plane which bisects the line segment joining the points

(- 3, - 3, 4)

and

(3, 7, 6)

at right angles, passes through which one of the following points?

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

X Y -

plane divides the line joining the points

A (2, 3, - 5)

and

B (- 1, - 2, - 3)

in the ratio

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

A spherical ball is kept at the corner of a rectangular room such that the ball touches two (perpendicular) walls and lies on the floor. If a point on the sphere is at distance of

9, 16, 25

from the two walls and the floor, then a possible radius of the sphere is

HARD

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

A (2, 3, - 4), B (- 3, 3, - 2), C (- 1, 4, 2)

and

D (3, 5, 1)

are the vertices of a tetrahedron. If

E, F, G

are the centroids of its faces containing the point

A,

then the centroid of the triangle

E F G

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

If a point

R (4, y, z)

lies on the line segment joining the points

P (2, - 3,4)

and

Q (8,0, 10),

then the distance of

R

from the origin is

EASY

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

The point

(1, - 3, 4)

lies in the octant

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

Let

A

and

B

be two points with position vectors

\vec{a}

and

\vec{b}

respectively and let

C

be a point dividing

A B

internally and the position vector of

C

A B

\vec{c} = λ \vec{a} + μ \vec{b},

then

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

Assertion $(A)$ : If $(- 1, 3, 2)$ and $(5, 3, 2)$ are respectively the orthocentre and circumcentre of a triangle, then $(3, 3, 2)$ is its centroid.

Reason $(R)$ : Centroid of the triangle divides the line segment joining the orthocentre and the circumcentre in the ratio $1 : 2$ .

Which one of the following is true?

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

If the origin and the points

P (2, 3, 4), Q (1, 2, 3)

and

R (x, y, z)

are co-planar then

HARD

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

For

x = (x_{1}, x_{2}, x_{3}) \in ℝ^{3}

, define

|x| = \sqrt{x_{1}^{2} + x_{2}^{2} + x_{3}^{2}}

. For

a = (1, 4, 4)

and

b =

(1, 0, 1)

, the maximum value of

|x|

satisfying

|x - a| = 2 |x - b|

MEDIUM

Mathematics>Coordinate Geometry>Three Dimensional Geometry>Basics of 3D Geometry

The shortest distance from the origin to a variable point on the sphere

{(x - 2)}^{2} + {(y - 3)}^{2} + {(z - 6)}^{2} = 1

Let 3, 4, -1 and (-1, 2, 3) are the end points of a diameter of sphere. Then the radius of the sphere is equal to

Important Questions on Three Dimensional Geometry

Learn and Prepare for any exam you want !

Let $(3, 4, - 1) a n d (- 1, 2, 3)$ are the end points of a diameter of sphere. Then the radius of the sphere is equal to