Let $ABCD$ be a circumscribed (or tangential) quadrilateral. Prove that the circles in the two triangles $ABC$ and $ADC$ are tangent to each other.

From a point $P$ outside a circle, $PAB$ is a secant and $PT$ is a tangent to the circle, where $A, B$ and $T$ are points on the circle. If $PT=5 cm, PA=4 cm$ and $AB=x cm$, then $x$ is equal to :

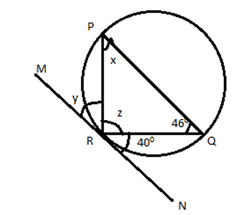
In the given figure, $\angle QRN=40°, \angle PQR=46°$ and $MN$ is a tangent at $R$. What is the value(in degrees) of $x, y$ and $z$ respectively?

A circle can have _____ parallel tangents at the most.

A tangent to a circle intersects it in _____ point(s). [Answer in words]

A circle may have _____ parallel tangents.

A circle can have _____ tangents.(zero/one/two/infinite)

A line intersecting a circle in two points is called a _____.

A line intersecting a circle in two distinct points is called a _____.

A tangent to a circle intersects it in _____ point(s). ( Write answer in words)

A tangent to a circle is a line that intersects the circle at only _____ point.

There is _____ tangent to a circle passing through a point lying inside the circle.

(Mention your answer in digits)

The common point of a _____ to a circle and the circle is called the Point of Contact.