Let $A_{\mathrm{n}}$ be the area enclosed by the $n^{\mathrm{th}}$ orbit in a hydrogen atom. The graph of $\ln \left(\frac{A_{\mathrm{n}}}{A_1}\right)$ against $\ln \left(n\right)$

1. Atomic Model:

(i) Thomson’s Plum Pudding Model: According to this model most of the mass and the positive charge of an atom are uniformly distributed throughout the volume of the atom. Electrons are embedded in this uniform distribution. It was not accepted as it failed to explain the $\alpha -$particle scattering in the gold foil experiment.

(ii) Rutherford Model: According to this model most of the mass and all the positive charge of an atom is concentrated within a very small volume at the centre of the atom. This small volume is called the nucleus of the atom. The electrons revolve around this positively charged centre. This model failed because according to the classical theory of electromagnetism, an accelerating charged particle emits electromagnetic waves. So, the revolving electrons having centripetal acceleration should emit electromagnetic waves, lose their energy and crash into the nucleus. Rutherford was not able to come up with an explanation for this, hence the model was not accepted.

(iii) Bohr Model of Hydrogen and Hydrogen-like Species: This model is based on the following postulates.

(a) The electrons revolve around the nucleus in stationary orbits.

(b) An electron doesn’t emit electromagnetic radiation when it is in these stationary orbits.

(c) A stationary orbit is that in which the angular momentum of the electron about the nucleus is an integral multiple of h2π.

$mvr=n\frac{h}{2\pi }, \left[n=1,2,3,\left(n\ne 0\right)\right]$

(d) The radius of any stationary orbit cannot take up any random continuous values, instead, it is quantized. The same is true for the velocity and energy of the electron.

$r_n=\frac{n^2}{Z}{a}_0$, $a_0=0.529 Å$ [Radius of nth orbit]

vn=znv0, $v_0=2.19\times {10}^6 \mathrm{m}\mathrm{ }{\mathrm{s}}^{-1}$ [Orbital velocity of the electron in the nth orbit]

$E_n=E_1\frac{Z^2}{n^2}\text{,} E_1=-13.6\mathrm{ }\mathrm{eV}$  [Energy of the electron]

2. Hydrogen Spectrum:

Rydberg's formula: 1λ=R1n12-1n22, [Wavelength corresponding to spectral lines]

Total number of emission spectral lines -

From energy level n to $1\mathrm{ }=\frac{n\left(n-1\right)}{2}$

From energy level n to $m=\left(\frac{\left(n-m\right)\left(n-m+1\right)}{2}\right)$

Excitation potential for a transition from $n_1\to n_2=\frac{E_{{\mathrm{n}}_2}-E_{{\mathrm{n}}_1}}{ e }$

Ionization Potential $=\frac{-E_{\mathrm{n}}}{ e }$

3. If the effect of motion of nucleus is considered:

$r_{\mathrm{n}}=\left(0.529Å\right)\frac{n^2}{Z}\frac{m}{\mu }$

$E_{\mathrm{n}}=\left(-13.6 \mathrm{eV}\right)\frac{Z^2}{n^2}\frac{\mu }{m}$

Here the reduced mass of the system (nucleus and electron)

$\mu =\frac{Mm}{\left(M+m\right)}$, M is the mass of the nucleus, m is the mass of the electron.

4. X-Ray:

X-rays are produced when high-speed electrons bombard on a metal target of high atomic mass and high melting point.

These are short-wavelength $\left(0.01 Å \mathrm{to} 100 Å\right)$ electromagnetic radiations.

These are not affected by electric and magnetic fields.

They can cause photoelectric emission.

(i) Continuous X-ray: The continuous $x$-rays are produced due to retardation of electrons inside the metal target.

The cutoff wavelength for x-rays in an x-ray tube is

${\lambda }_{\min }=\frac{hc}{e{V}_0}=\frac{12400}{ V_0\left(\mathrm{volt}\right)} Å$

The corresponding maximum frequency is $v_{\mathrm{m}}=\frac{eV}{h}$,

e=electron charge; $V=$accelerating potential; ${\lambda }_{\min }=$minimum wavelength of x-rays; $v_{\mathrm{m}}=$maximum frequency of $x$-rays.

The intensity of $x$-rays depends on the number of electrons hitting the target.

(ii) Characteristic $x$-ray: Characteristic $x$-rays are produced by knocking off electrons from the inner shells of the target atoms.

For $K_{\alpha }, \lambda =\frac{hc}{E_{\mathrm{K}}-E_{\mathrm{L}}}$, For $K_{\beta , } \lambda =\frac{hc}{E_{\mathrm{L}}-E_{\mathrm{M}}}$

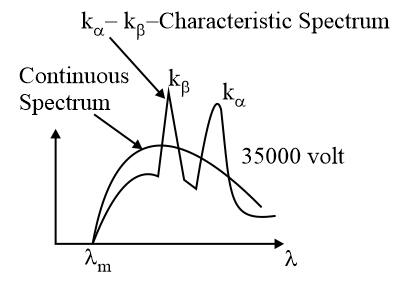
(iii) Moseley's law for characteristic $x$-rays:

$\sqrt{v}=a\left(z-b\right)$

Z= atomic number of target

v= frequency of the characteristic spectrum

$b=$ screening constant (for K- series b=1, $L$ series b=7.4)

$a=$ proportionality constant