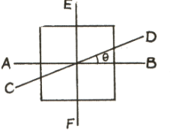
Let $\mathrm{I}$ be the moment of inertia, of a uniform square plate about an axis $\mathrm{AB}$  passes through its centre and is parallel to two of its sides. $\mathrm{CD}$ is a line in the plane of the plate that passes through the centre of the plate and makes an angle $\theta$ with $\mathrm{AB}$  as shown in the figure. The moment of inertia of the plate about the axis $\mathrm{CD}$ is then equal to

The ratio of the radii of gyration of a circular disc and a circular ring of the same masses and radii about their respective axis is:

Moment of inertia of a uniform circular disc about a diameter is $\mathrm{I}$. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be:

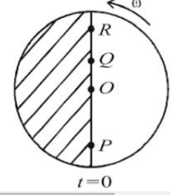
Consider a disc rotating in the horizontal plane with a constant angular speed $\omega$ about its centre O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the $Y-Z$  plane and is same for both pebbles with respect to the disc. Assume that :
(i) they land back on the disc before the disc has completed $\frac{1}{8}$​ rotation,
(ii) their range is less than half the disc radius, and
(iii)$\mathrm{\omega }$remains constant throughout. 

A thin rod of length `L` and mass `M` is bent at its midpoint into two halves so that the angle between them is `$90°$`. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is

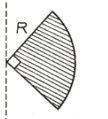
One quarter sector is cut from a uniform circular disc of radius $\mathrm{R}$ This sector has mass $\mathrm{M}$ It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is.