HARD

Earn 100

Let $a, b, c$ be in AP such that $|a| < 1, |b| < 1, |c| < 1$ . If $x = 1 + a + a^{2} + . . . t o \infty$ , $y = 1 + b + b^{2} + . . . t o \infty$ and $z = 1 + c + c^{2} + . . . \infty$ , then $x, y, z$ are in

50% studentsanswered this correctly

Important Questions on Sequences and Series

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

a, b

and

c

be the

7^{t h}, 11^{t h}

and

13^{t h}

terms respectively of a non-constant A.P. If these are also the three consecutive terms of a G.P., then

\frac{a}{c}

is equal to:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

The quotient when

1 + x^{2} + x^{4} + . . . + x^{34}

is divided by

1 + x + x^{2} + . . . + x^{17}

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

C_{0}

be a circle of radius

1

. For

n \geq 1,

let

C_{n}

be a circle whose area equals the area of a square inscribed in

C_{n - 1}

. Then

(\sum_{u = 0}^{\infty} area (C_{i}))

equals,

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

a, b

and

c

be in

G . P .

with common ratio

r,

where

a \neq 0

and

0 < r \leq \frac{1}{2} .

3 a, 7 b

and

15 c

are the first three terms of an

A . P .,

then the

4^{t h}

term of this

A . P .

is :

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progression

The product of three consecutive terms of a

G . P .

512

. If

4

is added to each of the first and the second of these terms, the three terms now form an

A . P .

, then the sum of the original three terms of the given

G . P .

is :

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

If three distinct numbers

a, b, c

are in G.P. and the equations

a x^{2} + 2 b x + c = 0

and

d x^{2} + 2 e x + f = 0

have a common root, then which one of the following statements is correct?

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progression

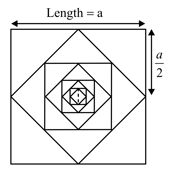
Let $S_{1}$ be the sum of areas of the squares whose sides are parallel to coordinate axes. Let $S_{2}$ be the sum of areas of the slanted squares as shown in the figure. Then $S_{1} / S_{2}$ is

Question Image

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progression

The product

2^{\frac{1}{4}} \cdot 4^{\frac{1}{16}} \cdot 8^{\frac{1}{48}} \cdot 16^{\frac{1}{128}} \cdot . . . .

\infty

is equal to:

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progression

The number of real solutions of the equation

\sin^{- 1} (\sum_{i = 1}^{\infty} x^{i + 1} - x \sum_{i = 1}^{\infty} {(\frac{x}{2})}^{i}) = \frac{π}{2} - \cos^{- 1} (\sum_{i = 1}^{\infty} {(- \frac{x}{2})}^{i} - \sum_{i = 1}^{\infty} {(- x)}^{i})

lying in the interval

(- \frac{1}{2}, \frac{1}{2})

is____.

(Here, the inverse trigonometric functions

\sin^{- 1} x & \cos^{- 1} x

assume values in

[- \frac{π}{2}, \frac{π}{2}] & [0, π]

respectively.)

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

The sum of first

20

terms of the sequence

0.7, 0.77, 0.777, . . . . . .,

is :

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

α, β

and

γ

are three consecutive terms of a non-constant G.P. Such that the equations

α x^{2} + 2 β x + γ = 0

and

x^{2} + x - 1 = 0

have a common root, then

α (β + γ)

is equal to:

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progression

If $m$ is the $A . M .$ of two distinct real numbers $I$ and $n$ $(I, n > 1)$ and $G_{1}, G_{2} and G_{3}$ are three geometric means between $I and n$ , then $G_{1}^{4} + 2 G_{2}^{4} + G_{3}^{4}$ equals

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progression

If the sum of an infinite GP be

9

and sum of first two terms be

5

then their common ratio is …..

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

If the

2^{n d}, 5^{t h}

and

9^{t h}

terms of a non-constant arithmetic progression are in geometric progression, then the common ratio of this geometric progression is

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

The greatest positive integer

k,

for which

49^{k} + 1

is a factor of the sum

49^{125} + 49^{124} + \dots + 49^{2} + 49 + 1,

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

a_{n}

be the

n^{t h}

term of a G.P. of positive terms. If

\sum_{n = 1}^{100} a_{2 n + 1} = 200

and

\sum_{n = 1}^{100} a_{2 n} = 100,

then

\sum_{n = 1}^{200} a_{n}

is equal to:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

x = \sum_{n = 0}^{\infty} {(- 1)}^{n} \tan^{2 n} θ

and

y = \sum_{n = 0}^{\infty} \cos^{2 n} θ,

for

0 < θ < \frac{π}{4},

then:

MEDIUM

Mathematics>Algebra>Sequences and Series>Geometric Progression

The sum of the

3^{r d}

and the

4^{t h}

terms of a

G . P .

60

and the product of its first three terms is

1000.

If the first term of this

G . P .

is positive, then its

7^{t h}

term is:

HARD

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

b_{i} > 1

for

i = 1, 2, \dots ., 101 .

Suppose

\log_{e} b_{1}, \log_{e} b_{2}, \dots . ., \log_{e} b_{101}

are in Arithmetic Progression (A.P.) with the common difference

\log_{e} 2 .

Suppose

a_{1}, a_{2}, \dots ., a_{101}

are in A.P. such that

a_{1} = b_{1}

and

a_{51} = b_{51} .

t = b_{1} + b_{2} + \dots + b_{51}

and

s = a_{1} + a_{2} + \dots + a_{51}

, then

EASY

Mathematics>Algebra>Sequences and Series>Geometric Progression

Let

a_{1}, a_{2}, {\dots . . a}_{10}

be a G.P. If

\frac{a_{3}}{a_{1}} = 25,

then

\frac{a_{9}}{a_{5}}

equals:

Let a,b,c be in AP such that a<1, b<1, c<1. If x=1+a+a2+...to ∞, y=1+b+b2+...to ∞ and z=1+c+c2+...∞, then x, y, z are in

Important Questions on Sequences and Series

Learn and Prepare for any exam you want !

Let $a, b, c$ be in AP such that $|a| < 1, |b| < 1, |c| < 1$ . If $x = 1 + a + a^{2} + . . . t o \infty$ , $y = 1 + b + b^{2} + . . . t o \infty$ and $z = 1 + c + c^{2} + . . . \infty$ , then $x, y, z$ are in