MEDIUM
Earn 100
Let the vectors and represent the sides of a regular hexagon.
Statement I:
Statement II: and
(a)Statement is true, statement is also true and statement is the correct explanation of statement .
(b)Statement is true, statement is also true and statement is not the correct explanation of statement .
(c)Statement is true, statement is false.
(d)Statement is false, statement is true.
43.4% studentsanswered this correctly
Important Questions on Mathematical Methods
HARD
EASY
MEDIUM
EASY
MEDIUM
EASY
HARD
HARD
HARD
EASY
HARD
MEDIUM
HARD
EASY
HARD
MEDIUM
HARD
Given, and Let be a vector such that and the angle between and be . Then is equal to:
HARD
HARD
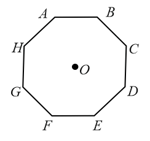
In an octagon of equal side, what is the sum of if,