Lurking alligators. An alligator waits for prey by floating with only the top of its head exposed. So, the prey cannot easily see it. One way it can adjust the extent of sinking is by controlling the size of its lungs. Another way may be by swallowing stones (gastrolithes) that then reside in the stomach. In the figure shows a highly simplified model (a "rhombohedron gater") of mass $145 \mathrm{kg}$ that roams with its head partially exposed. The top head surface has area $0.15 {\mathrm{m}}^2$. If the alligator were to swallow stones with a total mass of $1.0\%$ of its body mass (a typical amount), how far would it sink ?

 

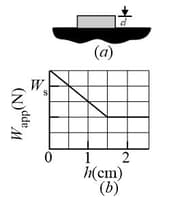
In the figure, a rectangular block is gradually pushed face down into a liquid. The block has height $d$; on the bottom and top the face area is $A=8.00 {\mathrm{cm}}^2$. In the figure, gives the apparent weight $W_{\mathrm{app}}$ of the block as a function of the depth $h$ of its lower face. The scale on the vertical axis is set by $W_{\mathrm{s}}=0.20 \mathrm{N}$. What is the density of the liquid ?

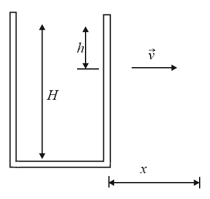
In the figure, shows a stream of water flowing through a hole at depth $h=12 \mathrm{cm}$ in a tank holding water to height $H=40 \mathrm{cm}$. (a) At what distance $x$ does the stream strike the floor ? (b) At what depth should a second hole be made to give the same value of $x$? (c) At what depth should a hole be made to maximize $x$ ?

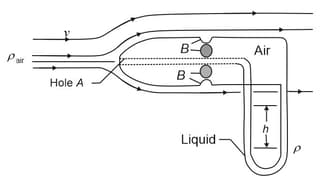
A pivot tube in the figure is used to determine the air-speed of an aeroplane. It consists of an outer tube with a number of small holes B (four are shown) that allow air into the tube; that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that $v_{\mathrm{A}}=0$. At B, however, the speed of the air presumably equals the airspeed $v$ of the plane. (a) Use Bernoulli's equation to show that

$v=\sqrt{\frac{2\rho gh}{{\rho }_{\mathrm{air}}}}$,

Where $\rho$ is the density of the liquid in the U-tube and $h$ is the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference $h$ is $20.0 \mathrm{cm}$. What is the plane's speed relative to the air ? The density of the air is $1.03 \mathrm{kg} {\mathrm{m}}^{-3}$ and that of alcohol is $810 \mathrm{kg} {\mathrm{m}}^{-3}$.

Models of torpedoes are sometimes tested in a horizontal pipe of flowing water, much as a wind tunnel is used to test model airplanes. Consider a circular pipe of internal diameter $25.0 \mathrm{cm}$ and a torpedo model aligned along the long axis of the pipe; The model has a $6.00 \mathrm{cm}$ diameter and is to be tested with water flowing past it at $2.00 \mathrm{m} {\mathrm{s}}^{-1}$. (a) with what speed must the water flow in the part of the pipe that is unconstricted by the model? (b) What will the pressure difference be between the constricted and unconstricted parts of the pipe?