Mass is non-uniformly distributed over the rod of length $l$. Its linear mass density varies linearly with length as $\lambda =k{x}^2$. The position of centre of mass (from lighter end) is given by-

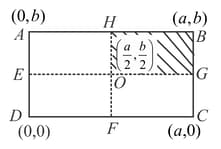
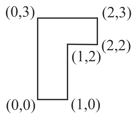
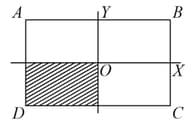
A uniform rectangular thin sheet $ABCD$ of mass $M$ has length $a$ and breadth $b$, as shown in the figure. If the shaded portion $HBGO$ is cut-off, the coordinates of the centre of mass of the remaining portion will be:

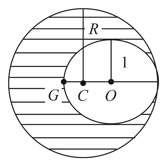
As shown in figure, when a spherical cavity (centred at $O$ ) of radius $1$ is cut out of a uniform sphere of radius $R$ (centred at $C$ ), the centre of mass of remaining (shaded part of sphere is at $G,$ i.e., on the surface of the cavity. $R$ can be determined by the equation:

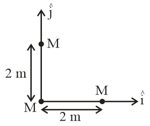
Three identical spheres, each of mass $M,$ are placed at the corners of a right angle triangle with mutually perpendicular sides equal to $2 \mathrm{m}$ (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of centre of mass.

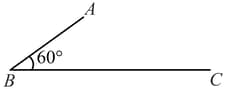
In the figure shown $ABC$ is a uniform wire. If the center of mass of the wire lies vertically below point $A$, then $\frac{BC}{AB}$ is close to

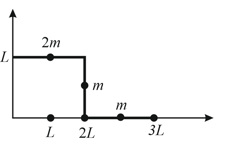
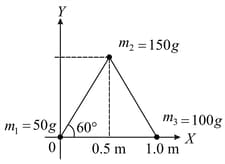
Three point particles of masses $1.0 \mathrm{k}\mathrm{g}, 1.5 \mathrm{kg}$ and $2.5 \mathrm{k}\mathrm{g}$ are placed at three corners of a right angle triangle of sides $4.0 \mathrm{c}\mathrm{m}, 3.0 \mathrm{c}\mathrm{m}$ and $5.0 \mathrm{c}\mathrm{m}$ as shown in the figure. The centre of mass of the system is at a point:

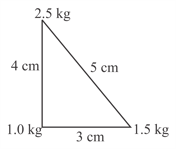
Figure shows a rectangular copper plate with its centre of mass at the origin $O$ and side $AB=2BC=2 \mathrm{m}.$ If a quarter part of the plate (shown as shaded) is removed, the centre of mass of the remaining plate would lie at

Three particles of masses $50 \mathrm{g}$, $100\mathrm{ }\mathrm{g}$ and $150\mathrm{ }\mathrm{g}$ are placed at the vertices of an equilateral triangle of side $1 \mathrm{m}$ (as shown in the figure). The $\left(\mathrm{x},\mathrm{y}\right)$ coordinates of the centre of mass will be: