Neither it's the longest one nor it's the shortest one of the lengths of the diagonal of an octagon you know is $\mathrm{d}$ and each side of the same octagon is $\mathrm{s},$ find the area of the octagon in terms of the side and the known diagonal of the regular octagon.

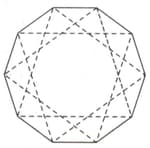
In the given diagram, a regular octagon is inscribed in a circle in which four diagonals are connecting the opposite vertices of the octagon. After that a square is formed by connecting the alternate vertices of the octagon then another square is formed by joining the mid-points of the first square and then finally another square is formed by joining the mid-points of the previous square. This square is shown as the shaded region. If the area of the shaded region is $1$ sq. cm, find the difference between the area of the circle and area of the octagon.

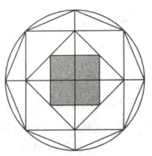
In the given figure a quadrilateral is formed by joining the alternate vertices of a regular octagon. If the area of the octagon be $2(\sqrt{2}-1) \mathrm{sq} \mathrm{cm},$ find the area of the square.

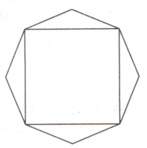
In the given figure, a concave equilateral octagon has each of its four acute internal angles equal to $30°$ and each of the two longer diagonals is $20 \mathrm{cm}.$ Find the area of the octagon, if the diagonals connecting the opposite vertices are perpendicular and bisect each other.

In the given figure, there are $4$ black and four white rhombi connected in such a way that one of their vertices is common, and they share two of their sides with the rhombi of either side without any overlapping. Each of the eight rhombi is congruent to each other. The total area of all the black rhombi (or shaded region) is $8 \mathrm{sq} \mathrm{cm},$ Find the area of the smallest possible octagon in which the following figure can be inscribed as it is.

In the given diagram, some diagonals of a regular decagon are intersecting such that they form another small decagon inside the original decagon. If each side of the larger decagon be $2 \mathrm{cm},$ find the side of the smaller decagon.