HARD

Earn 100

One mole of a diatomic ideal gas is taken through a cyclic process starting from point A. The process A → B is an adiabatic compression. B → C is isobaric expansion, C → D an adiabatic expansion and D → A is isochoric respectively.
The volume ratios are given to be $\frac{V_{A}}{V_{B}} = 16$ and $\frac{V_{C}}{V_{B}} = 2$ and the temperature at A is $T_{A} = 300 K$ . The efficiency of the cyclic process (in $%$ ) is $α$ . Find value of $[α],$ where $[]$ is the greatest integer function.

50% studentsanswered this correctly

Important Questions on Heat and Thermodynamics

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

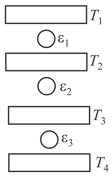
Three Carnot engines operate in series between a heat source at a temperature

T_{1}

and a heat sink at temperature

T_{4}

(see figure). There are two other reservoirs at temperature

T_{2}

and

T_{3},

as shown, with

T_{1} > T_{2} > T_{3} > T_{4} .

The three engines are equally efficient if:

Question Image

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot engine has an efficiency of

\frac{1}{6} .

When the temperature of the sink is reduced by

62 ℃

, its efficiency is doubled. The temperatures of the source and the sink are, respectively,

HARD

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

Two ideal Carnot engines operate in a cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures,

T_{1}

and

T_{2}

. The temperature of the hot reservoir of the first engine is

T_{1}

and the temperature of the cold reservoir of the second engine is

T_{2}

T

is the temperature of the sink of the first engine which is also the source for the second engine. How is

T

related to

T_{1}

and

T_{2}

, if both the engines perform an equal amount of work?

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A refrigerator works between

4^{o} C

and

30^{o} C

. It is required to remove

600

calories of heat every second in order to keep the temperature of the refrigerated space constant. The power required is:

(Take

1

cal =

4 .2

Joules)

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot's engine having an efficiency of

\frac{1}{10}

as heat engine, is used as a refrigerator. If the work done on the system is

10 J,

the amount of energy absorbed from the reservoir at lower temperature is

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

If minimum possible work is done by a refrigerator in converting 100 grams of water at

0 ° C

to ice, how much heat (in calories) is released to the surroundings at temperature

27 ° C

(Latent heat of ice

= 80 Cal / gram

) to the nearest integer?

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot engine having an efficiency of

\frac{1}{10}

is being used as a refrigerator. If the work done on the refrigerator is

10 J,

the amount of heat absorbed from the reservoir at a lower temperature is

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

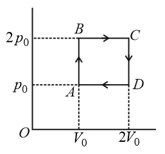
Helium gas goes through a cycle $A B C D A$ (consisting of two isochoric and two isobaric lines) as shown in figure. The efficiency of this cycle is approximately

Question Image

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

The coefficient of performance of a refrigerator is

5

. If the temperature inside the freezer is

- 20 ° C

, the temperature of the surrounding to which it rejects heat is:

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot freezer takes heat from water at

0^{o} C

inside it and rejects it to the room at a temperature of

27^{o} C .

The latent heat of ice is

336 \times 10^{3} J k g^{- 1} .

If 5kg of water at

0^{o} C

is converted into ice at

0^{o} C

by the freezer, then the energy consumed by the freezer is close to :

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

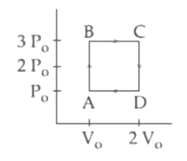
An engine operates by taking a monatomic ideal gas through the cycle shown in the figure. The percentage efficiency of the engine is close to

Question Image

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot engine, having an efficiency of

η = \frac{1}{10}

as heat engine, is used as a refrigerator. If the work done on the system is

10 J

, the amount of energy absorbed from the reservoir at a lower temperature is:

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

The efficiency of a Carnot engine depends upon

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A heat engine is involved with exchange of heat of

1915 J, - 40 J, + 125 J

and

- Q J

, during one cycle achieving and efficiency of

50.0 %

. The value of

Q

is:

MEDIUM

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A reservoir is at

827 ° C

and Carnot's engine takes a thousand

kilo calorie

of heat from it and exhausts it to a sink at

27 ° C

. What is the amount of work and the efficiency of the engine?

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

Two carnot engines

A

and

B

are connected in series in such a way that the work outputs are equal when the temperatures of hot and cold reservoirs of

A

are

800 K

and

T

, and of engine

B

are

T

and

300 K

, respectively. Then the temperature

T

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

An air conditioner

(A C)

removes heat at a rate of

1.2 kJ \sec^{- 1}

from a room. A power of

400 W

is required to run the

A C

. The coefficient of performance

(α)

of the

A C

10 %

of that of the refrigerator operating between outside and room temperature. If outside temperature is

37 ° C

, what will be room temperature?

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

A Carnot engine operates between two reservoirs of temperatures

900 K

and

300 K

. The engine performs

1200 J

of work per cycle. The heat energy (in

J

) delivered by the engine to the low temperature reservoir, in a cycle, is _____________

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

The temperature inside a refrigerator is

t_{2}^{o} C

and the room temperature is

t_{1}^{o} C

. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be

EASY

Physics>Heat and Thermodynamics>Heat and Thermodynamics>Carnot Engine Efficiency and Coefficient of Performance

Two carnot engines

A

and

B

are operated in series. The first one,

A,

receives heat at

T_{1} (= 600 K)

and rejects to a reservoir at temperature

T_{2} .

The second engine

B

receives heat rejected by the first engine and, in turn, rejects to a heat reservoir at

T_{3} (= 400 K) .

Calculate the temperature

T_{2}

if the work outputs of the two engines are equal:

Important Questions on Heat and Thermodynamics

Learn and Prepare for any exam you want !