MEDIUM

Earn 100

One mole of an ideal gas expands adiabatically from an initial state $(T_{A}, V_{0})$ to final state $(T_{f}, 5 V_{0})$ . Another mole of the same gas expands isothermally from a different initial state $(T_{B}, V_{0})$ to the same final state $(T_{f}, 5 V_{0})$ . The ratio of the specific heats at constant pressure and constant volume of this ideal gas is $γ$ . What is the ratio $\frac{T_{A}}{T_{B}}$ ?

80.46% studentsanswered this correctly

Important Questions on Thermodynamics

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then:

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A mixture of ideal gas containing

5

moles of monatomic gas and

1

mole of rigid diatomic gas is initially at pressure

P_{0},

volume

V_{0}

and temperature

T_{0} .

If the gas mixture is adiabatically compressed to a volume

\frac{V_{0}}{4}

, then the correct statement(s) is/are,
(Given

2^{1.2} = 2.3; 2^{3.2} = 9.2; R

is gas constant)

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

If a monoatomic gas is compressed adiabatically to

(1 / 27)

th of its initial volume, then its pressure becomes

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Consider one mole of helium gas enclosed in a container at initial pressure

P_{1}

and volume

V_{1}

. It expands isothermally to volume

4 V_{1}

. After this, the gas expands adiabatically and its volume becomes

32 V_{1}

. The work done by the gas during isothermal and adiabatic expansion processes are

W_{iso}

and

W_{a d i a},

\frac{W_{iso}}{W_{adia}} = f \ln (2)

, then

f

is _________ .

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

The bulk modulus of a gas is defined as,

B = \frac{- V d P}{d V}

. For an adiabatic process, the variation of

B

is proportional to

P^{n}

. For an ideal gas,

n

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

In an adiabatic process, the density of a diatomic gas becomes

32

times its initial value. The final pressure of the gas is found to be

n

times the initial pressure. The value of

n

is:

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

1

litre of dry air at STP expands adiabatically to a volume of

3

litres. If

γ = 1.40,

the work done by air is:

(3^{1.4} = 4.6555)

[Take air to be an ideal gas]

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of ideal gas goes through a process

P V^{3} =

constant, where

P

and

V

are pressure and volume respectively. Let

W

be the work done by the gas as its temperature is increased by

Δ T

. The value of

|W|

is (

R

is the universal gas constant)

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Two moles of an ideal monoatomic gas occupies a volume $V$ at $27^{o} C$ . The gas expands adiabatically to a volume $2 V$ . Calculate $(a)$ the final temperature of the gas and $(b)$ change in its internal energy.

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding P-V diagrams in column 3 of the table. Consider only the path from state

1

to state

2

W

denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic process. Here

γ

is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is

n

Column – 1	Column – 2	Column – 3
(I) $W_{1 \to 2} = \frac{1}{γ - 1} (P_{2} V_{2} - P_{1} V_{1})$	(i) Isothermal	(P)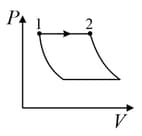
(II) $W_{1 \to 2} = - P V_{2} + P V_{1}$	(ii) Isochoric	(Q)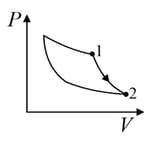
(III) $W_{1 \to 2} = 0$	(iii) Isobaric	(R)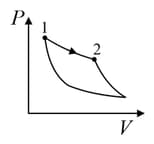
(IV) $W_{1 \to 2} = - n R T \ln (\frac{V_{2}}{V_{1}})$	(iv) Adiabatic	(S)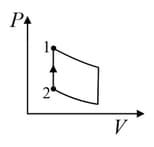

Which one of the following options correctly represents a thermodynamic process that is used as a correction in the determination of the speed of sound in ideal gas?

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An ideal monoatomic gas at

300 K

expands adiabatically to twice its volume. The final temperature of gas is

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of an ideal monatomic gas undergoes an adiabatic expansion in which its volume becomes eight times its initial value. If the initial temperature of the gas is

100 K

and the universal gas constant

R = 8.0 J mo l^{- 1} K^{- 1}

, then how much is the decrease in its internal energy (in

J

) ?

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

When a tyre pumped to a pressure

3.3375 atm

27 ° C

suddenly bursts, find its final temperature

(γ = 1.5)

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An engine takes in

5

moles of air at

20 ° C

and

1 atm

, and compresses it adiabatically to

1 / 10^{th}

of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be

X kJ

. The value of

X

to the nearest integer is:

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

The rapid changes in pressure and volume of an ideal gas under thermal isolation are governed by

T P^{- 2 / 5} =

constant. The gas may be ___ .

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

For an ideal gas with initial pressure and volume

p_{i}

and

V_{i}

respectively, a reversible isothermal expansion happens, when its volume becomes

V_{0}

. Then, it is compressed to its original volume

V_{i}

by a reversible adiabatic process. If the final pressure is

p_{f}

then which of the following statement(s) is/are true?

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A gas consisting of rigid molecules expands adiabatically such that r.m.s. speed of its molecules becomes half. The ratio of final and initial volumes of the gas is (ratio of specific heat capacities of the gas is

1.5

)

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding P-V diagrams in column 3 of the table. Consider only the path from state 1 to state 2. W denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic process. Here

γ

is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is

n

Column – 1	Column – 2	Column – 3
(I) $W_{1 \to 2} = \frac{1}{γ - 1} (P_{2} V_{2} - P_{1} V_{1})$	(i) Isothermal	(P)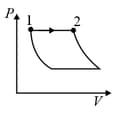
(II) $W_{1 \to 2} = - P V_{2} + P V_{1}$	(ii) Isochoric	(Q)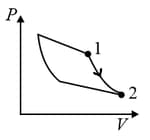
(III) $W_{1 \to 2} = 0$	(iii) Isobaric	(R)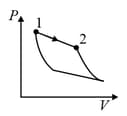
(IV) $W_{1 \to 2} = - n R T \ln (\frac{V_{2}}{V_{1}})$	(iv) Adiabatic	(S)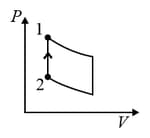

Which one of the following options is the correct combination?

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

The heat capacity of one mole an ideal is found to be

C_{V} = \frac{3 R (1 + a R T)}{2}

where

a

is constant. The equation obeyed by this gas during a reversible adiabatic expansion is:

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Consider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume

u = \frac{U}{V} \propto T^{4}

and pressure

p = \frac{1}{3} (\frac{U}{V})

. If the shell now undergoes an adiabatic expansion the relation between T and R is:

Important Questions on Thermodynamics

Learn and Prepare for any exam you want !