$PQ \text{and} PR$ are two infinite rays, $QAR$ is an arc. Point lying in the shaded region excluding the boundary satisfies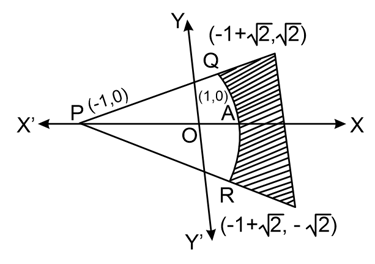

(where $\mathrm{i}=\sqrt{-1}$)

$\text{'}P\text{'}$ represents the variable complex number $z$. Find the locus of $P$. If $Re\left[\frac{z-1}{z+i}\right]=1$.

Let ${\theta }_1,{\theta }_2,\dots ,{\theta }_{10}$ be positive valued angles (in radian) such that ${\theta }_1+{\theta }_2+\cdots +{\theta }_{10}=2\pi$. Define the complex numbers $z_1=e^{i{\theta }_1}, z_k=z_{k-1}{e}^{i{\theta }_k}$ for $k=2,3,\dots ,10$, where $i=\sqrt{-1}$. Consider the statements $P$ and $Q$ given below:

$P:\left|z_2-z_1\right|+\left|z_3-z_2\right|+\cdots +\left|z_{10}-z_9\right|+\left|z_1-z_{10}\right|\le 2\pi$

$Q:\left|z_2^2-z_1^2\right|+\left|z_3^2-z_2^2\right|+\cdots +\left|z_{10}^2-z_9^2\right|+\left|z_1^2-z_{10}^2\right|\le 4\pi$

If $\left|z-z_1\right|=\left|z-z_2\right|$, then the locus of $z$ is 

Let $C$ be the circle in the complex plane with centre $z_0=\frac{1}{2}\left(1+3i\right)$ and radius $r=1$. Let $z_1=1+i$ and the complex number $z_2$ be outside circle $C$ such that $\left|z_1-z_0\right|\left|z_2-z_0\right|=1$. If $z_0, z_1$ and $z_2$ are collinear, then the smaller value of ${\left|z_2\right|}^2$ is equal to

The point $P\left(a,b\right)$ undergoes the following three transformations successively:
$\left(a\right)$ reflection about the line $y=x.$
$\left(b\right)$ translation through $2$ units along the positive direction of $x-$ axis.
$\left(c\right)$ rotation through angle $\frac{\pi }{4}$ about the origin in the anti-clockwise direction.

If the co-ordinates of the final position of the point $P$ are $\left(-\frac{1}{\sqrt{2}},\frac{7}{\sqrt{2}}\right)$, then the value of $2a+b$ is equal to: