HARD

IOQM - PRMO and RMO

IMPORTANT

Earn 100

$P S$ is a line segment of length $4$ unit and $O$ is the midpoint of $P S .$ A semicircular arc is drawn with $P S$ as diameter. Let $X$ be the midpoint of this arc. $Q$ and $R$ are points on the arc $P X S$ such that $Q R$ is parallel to $P S$ and the semicircular arc drawn with $Q R$ as diameter is tangent to $P S .$ What is the area of the region $Q X R O Q$ bounded by the two semicircular arcs?

Questions featured in Previous Year Papers on Previous Year Papers

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 30

For any real number

x,

let

[x]

denote the integer part of

x; {x}

be the fractional part of

x .

(\{x\} = x - [x])

. Let

A

denote the set of all real numbers

x

satisfying

\{x\} = \frac{x + [x] + [x + (\frac{1}{2})]}{20}

. If

S

is the sum of all numbers in

A,

find

[S]

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 29

Let

A B C

be an acute angled triangle with

A B = 15

and

B C = 8 .

Let

D

be a point on

A B

such that

B D = B C .

Consider points

E

A C

such that

∠ D E B = ∠ B E C .

α

denotes the product of all possible values of

A E,

find

\frac{[α]}{10}

, where

[α]

is the integer part of

α .

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 28

In a triangle

A B C,

it is known that

∠ A = 100 °

and

A B = A C .

The internal angle bisector

B D

has length

20

units. Find the length of

B C

to the nearest integer, given that

\sin 10 ° \approx 0.174 .

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 27

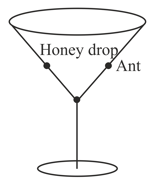
A conical glass is in the form of a right circular cone. The slant height is $21$ and the radius of the top rim of the glass is $14$ . An ant at the mid-point of a slant line on the outside wall of the glass sees a honey drop diametrically opposite to it on the inside wall of the glass (See the figure.). If $d$ the shortest distance it should crawl to reach the honey drop, what is the integer part of $d ?$ (ignore the thickness of the glass.)

Question Image

MEDIUM

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 26

A friction-less board has the shape of an equilateral triangle of side length

1

meter with bouncing walls along the sides. A tiny super bouncy ball is fired from vertex

A

towards the side

B C .

The ball bounces off the walls of the board nine times before it hits a vertex for the first time. The bounces are such that the angle of incidence equals the angle of reflection. The distance travelled by the ball in meters is of the form

\sqrt{N},

where

N

is an integer. What is the value of

N ?

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 25

Let

A B C

be an isosceles triangle with

A B = B C .

A trisector of

∠ B

meets

A C

D .

A B, A C

and

B D

are integers and

A B - B D = 3,

find

A C

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 24

For

n \geq 1,

let

a_{n}

be the number beginning with

n 9's

followed by

744;

e.g.,

a_{4} = 9999744 .

Define

f (n) = \max \{m \in N ∣ 2^{m} divides a_{n}\}

for

n \geq 1 .

Find

f (1) + f (2) + f (3) + \dots \dots . + f (10)

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-2 for PRMO>Chapter -1 - Previous Year Papers>Exercise 1>Q 22

In parallelogram

A B C D, A C = 10

and

B D = 28 .

The points

K

and

L

in the plane of

A B C D

move in such a way that

A K = B D

and

B L = A C .

Let

M

and

N

be the midpoints of

C K

and

D L,

respectively. What is the maximum value of

\cot^{2} (\frac{∠ B M D}{2}) + \tan^{2} (\frac{∠ A N C}{2})

Questions featured in Previous Year Papers on Previous Year Papers

Learn and Prepare for any exam you want !