Paired, bivariate data $(x, y)$ that is strongly correlated has a $y$ on $x$ line of best fit of $y=mx+c$. When $x=70$, an estimate for $y$ is $100$. When $x=100$, an estimate for $y$ is $140$
State if there is positive or negative correlation.

Paired, bivariate data $(x, y)$ that is strongly correlated has a $y$ on $x$ line of best fit of $y=mx+c$. When $x=70$, an estimate for $y$ is $100$. When $x=100$, an estimate for $y$ is $140$
The value of  $\overline{x}$ is $90$, find the value of $\overline{y}$.

Paired, bivariate data $(x, y)$ that is strongly correlated has a $y$ on $x$ line of best fit of $y=mx+c$. When $x=70$, an estimate for $y$ is $100$. When $x=100$, an estimate for $y$ is $140$
When $x=60$ find an estimate for the value of $y$, given that this is interpolation.

The temperature, $T°\mathrm{C}$, of liquid in a chemical reaction is a function of time, $t$, in seconds, where $t$ is the time from when the experiment started. The relationship is given by the equation:
$f\left(x\right)=\left\{\begin{array}{ll}40+2t& 0\le t\le 30\\ 130-t& 30\le t\le 60\end{array}\right.$
Find the initial temperature of the liquid and the temperature of the liquid after $60 \mathrm{secs}$.

1: The temperature $T°\mathrm{C}$, of liquid in a chemical reaction is a function of time $t$, in seconds, where $t$ is the time from when the experiment started. The relationship is given by the equation:
$f\left(x\right)=\left\{\begin{array}{ll}40+2t& 0\le t\le 30\\ 130-t& 30\le t\le 60\end{array}\right.$
Find the maximum temperature that the liquid reaches.

The temperature,$T°\mathrm{C}$, of liquid in a chemical reaction is a function of time, $t$, in seconds, where $t$ is the time from when the experiment started. The relationship is given by the equation:
$f\left(x\right)=\left\{\begin{array}{ll}40+2t& 0\le t\le 30\\ 130-t& 30\le t\le 60\end{array}\right.$
Find the initial temperature of the liquid. Sketch a graph of $T$ as a function of $t$.

The temperature,$T°\mathrm{C}$, of liquid in a chemical reaction is a function of time, $t$, in seconds, where $t$ is the time from when the experiment started. The relationship is given by the equation:
$f\left(x\right)=\left\{\begin{array}{ll}40+2t& 0\le t\le 30\\ 130-t& 30\le t\le 60\end{array}\right.$

Ten teenagers were asked their age and the number of brothers and sisters they have. The data are shown in the scatter diagram below, where $x$ represents the teenager's age and $y$ represents the number of brothers and sisters that they have.

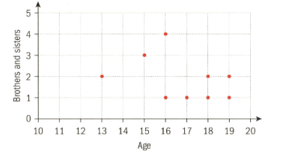
Use the scatter diagram to copy and complete the following table.

$\begin{array}{|ccccccccccc|}\hline x& 13& 14& 15& 16& 16& 17& 18& 18& 19& 19\\ y& & & & & 4& & & 2& 1& \\ \hline\end{array}$

Ten teenagers were asked their age and the number of brothers and sisters they have. The data are shown in the scatter diagram below, where $x$ represents the teenager's age and $y$ represents the number of brothers and sisters that they have.

$\begin{array}{|lllllllllll|}\hline x& 13& 14& 15& 16& 16& 17& 18& 18& 19& 19\\ y& 2& 0& 3& 1& 4& 1& 1& 2& 1& 2\\ \hline\end{array}$

Calculate the Pearson product moment correlation coefficient for this data.