Particles $P$ and $Q,$ of masses $0.6 \mathrm{kg}$ and $0.4 \mathrm{kg},$ respectively, are joined by a light inextensible string that passes over a small, smooth, fixed pulley. The particles are held at rest with the string taut and its straight parts vertical. Initially, both particles are $1.45 \mathrm{m}$ above the ground and $0.25 \mathrm{m}$ below the pulley. The system is released from rest.

Find the speed of$P$ and $Q$ reaches the pulley. The string then breaks and $\mathrm{P}$ falls to the ground.  Find the time from when the system is released to when $P$ hits the ground.

Particles $A$ and $B,$ each of mass $0.5 \mathrm{kg},$ are attached to the ends of a light inextensible string. Particle $A$ is held on a smooth slope inclined at $30°$ to the horizontal. The string passes over a small smooth pulley at the top of the slope and particle $B$ hangs vertically below the pulley. Particle $A$ is released and moves up the slope.Particle $B$hits the ground after $1.2 s$ It then stays on the ground and particle $A$ travels further up the slope. Particle A does not reach the pulley in the subsequent motion.

Find the acceleration of particle $A$ up the slope. 

Particles $A$ and $B,$ each of mass $0.5 \mathrm{kg},$ are attached to the ends of a light inextensible string. Particle $A$ is held on a smooth slope inclined at $30°$ to the horizontal. The string passes over a small smooth pulley at the top of the slope and particle $B$ hangs vertically below the pulley. Particle $A$ is released and moves up the slope.Particle  $B$ hits the ground after$1.2 \mathrm{s}$  It then stays on the ground and the particle $A$ travels further up the slope. Particle $A$ does not reach the pulley in the subsequent motion.

Find the distance travelled by particle $A,$ from when it is released to when it comes to instantaneous rest.

Particles $A$ and $B,$ of masses $0.5 \mathrm{kg}$ and $2.5 \mathrm{kg},$ respectively, are attached to the ends of a light inextensible string. Particle $A$ is held on a rough horizontal surface with coefficient of friction $0.2.$ The string passes over a small smooth pulley at the edge of the surface, at a distance $5 \mathrm{m}$ from particle $A.$ Particle $B$ hangs vertically below the pulley. Particle $A$ is released and particle $B$ descends $1 \mathrm{m}$ to reach the ground. When particle $B$ reaches the ground, it stays there. Find the time taken from the start until particle $A$ comes to instantaneous rest.

A crate of mass $20 \mathrm{kg}$ is pulled vertically upwards using a rope that passes over a first pulley, under a second pulley and over a third pulley. At the other end of the rope there is a ball of mass $30 \mathrm{kg}.$ Each pulley has mass $m \mathrm{kg}.$ The first and third pulleys are fixed at the same horizontal level and are $4 \mathrm{m}$ apart. The second pulley is an equal distance from the first and third pulleys and hangs at a distance $2 \mathrm{m}$ below them. It is not fixed, but it does not move.

What modelling assumptions need to be made? Which of these assumptions is unlikely to affect the equilibrium of the second pulley?

A crate of mass $20 \mathrm{kg}$ is pulled vertically upwards using a rope that passes over a first pulley, under a second pulley and over a third pulley. At the other end of the rope there is a ball of mass $30 \mathrm{kg}.$ Each pulley has mass $m \mathrm{kg}.$ The first and third pulleys are fixed at the same horizontal level and are $4 \mathrm{m}$ apart. The second pulley is an equal distance from the first and third pulleys and hangs at a distance $2 \mathrm{m}$ below them. It is not fixed, but it does not move.

Find the value of $m.$

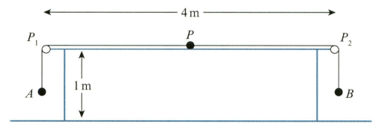
A light inextensible string of length $5.28 \mathrm{m}$ has particles $A$ and $B,$ of masses $0.25 \mathrm{kg}$ and $0.75 \mathrm{kg}$ respectively, attached to its ends. Another particle, $P,$ of mass $0.5 \mathrm{kg},$ is attached to the mid-point of the string. Two small smooth pulleys $P_1$ and $P_2$ are fixed at opposite ends of a rough horizontal table of length $4 \mathrm{m}$ and height $1 \mathrm{m}.$ The string passes over $P_1$ and $P_2$ with particle $A$ held at rest vertically below $P_1,$ the string taut and $B$ hanging freely below $P_2.$ Particle $P$ is in contact with the table halfway between $P_1$ and $P_2$ (see diagram). The coefficient of friction between $P$ and the table is $0.4.$ Particle $A$ is released and the system starts to move with constant acceleration of magnitude $a \mathrm{m}{\mathrm{s}}^{-2}.$ The tension in the part $AP$ of the string is $T_A N$ and the tension in the part $PB$ of the string is $T_B\mathit{ }N.$

Find $T_A$ and $T_B$ in terms of $a.$

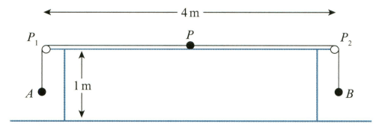
A light inextensible string of length $5.28 \mathrm{m}$ has particles $A$ and $B,$ of masses $0.25 \mathrm{kg}$ and $0.75 \mathrm{kg}$ respectively, attached to its ends. Another particle, $P,$ of mass $0.5 \mathrm{kg},$ is attached to the mid-point of the string. Two small smooth pulleys $P_1$ and $P_2$ are fixed at opposite ends of a rough horizontal table of length $4 \mathrm{m}$ and height $1 \mathrm{m}.$ The string passes over $P_1$ and $P_2$ with particle $A$ held at rest vertically below $P_1,$ the string taut and $B$ hanging freely below $P_2.$ Particle $P$ is in contact with the table halfway between $P_1$ and $P_2$ (see diagram). The coefficient of friction between $P$ and the table is $0.4.$ Particle $A$ is released and the system starts to move with constant acceleration of magnitude $a \mathrm{m}{\mathrm{s}}^{-2}.$ The tension in the part $AP$ of the string is $T_A N$ and the tension in the part $PB$ of the string is $T_B\mathit{ }N.$

Show, by considering the motion of $P$ that $a=2.$

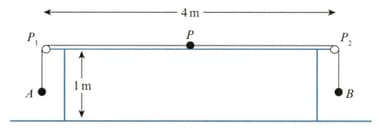
A light inextensible string of length $5.28 \mathrm{m}$ has particles $A$ and $B,$ of masses $0.25 \mathrm{kg}$ and $0.75 \mathrm{kg}$ respectively, attached to its ends. Another particle, $P,$ of mass $0.5 \mathrm{kg},$ is attached to the mid-point of the string. Two small smooth pulleys $P_1$ and $P_2$ are fixed at opposite ends of a rough horizontal table of length $4 \mathrm{m}$ and height $1 \mathrm{m}.$ The string passes over $P_1$ and $P_2$ with particle $A$ held at rest vertically below $P_1,$ the string taut and $B$ hanging freely below $P_2.$ Particle $P$ is in contact with the table halfway between $P_1$ and $P_2$ (see diagram). The coefficient of friction between $P$ and the table is $0.4.$ Particle $A$ is released and the system starts to move with constant acceleration of magnitude $a \mathrm{m}{\mathrm{s}}^{-2}.$ The tension in the part $AP$ of the string is $T_A N$ and the tension in the part $PB$ of the string is $T_B\mathit{ }N.$

Find the speed of the particles immediately before $B$ reaches the floor.