Points $A, B$ and $C$ lie on a circle with center $O$ such that $A, B$ and $C$ all fall within the same semicircle. Prove that $\angle \mathrm{ABC}= 180°-\frac{1}{2}\angle \mathrm{AOC}$.

.

 

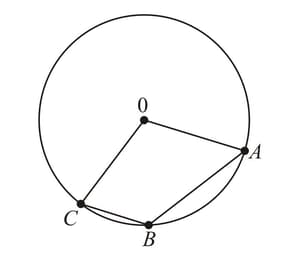
Points $P, X$ and $Y$ lie on the circumference of a circle. The tangents to the circle at $X$ and $Y$ meet at $Q$ Let $O$ be the center of the circle. Prove that $\angle \mathrm{XPY}= \frac{1}{2}(180°-\angle \mathrm{XQY})$.

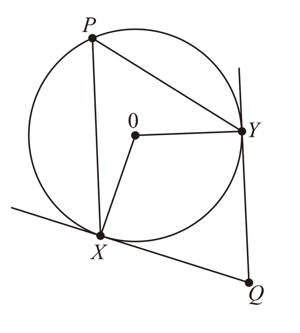
Points $B, D$ and $E$ lie on a circle. $ABC$ is a tangent to the circle at $B$. $DE$ is parallel to $ABC$. Prove that:  $△\mathrm{BDE}$, is isosceles.

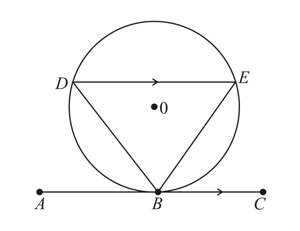
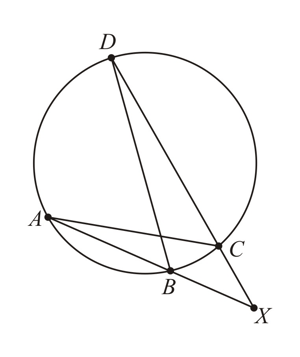
$A, B, C$ and $D$ lie on the circumference of a circle, and when the line segments $AB$ and $DC$ are extended they meet at $X$, outside the circle.

Prove that $△\mathrm{ACX}$, is similar to $△\mathrm{DBX}$.

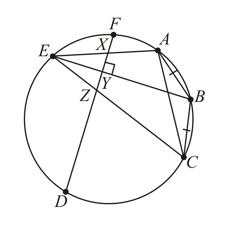
$A, B, C, D, E$ and $F$ lie on the circumference of a circle, with $AB = BC$ and $DF$ perpendicular to $BE, AE, BE$ and $CE$ meet $DF$ at $X, Y$ and $Z$ respectively. Prove that $\angle \mathrm{EXY} = \angle \mathrm{EZY}$

.

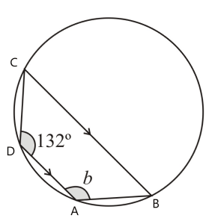
Find the size of marked angles.

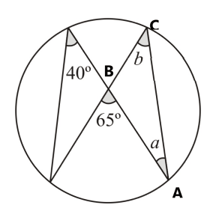
Find the size of marked angles.

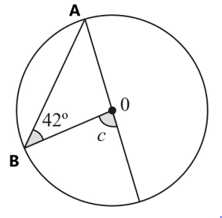
Find the size of marked angles.

Justify your answers.

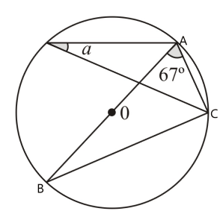
Find the size of marked angles.

Justify your answers.