Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Important Questions on Circles
Prove that the tangents drawn from an external point to a circle subtend equal angles at the centre of the circle.
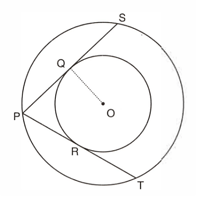
In the figure given below, there are two concentric circles with centre . and are tangents to the inner circle from a point lying on the outer circle. If , find the length of .
In the figure given below, is tangent from an external point to a circle with centre and cuts the circle at and is a diameter. If and is a point on the circle, find .
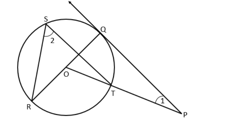
In the adjoining figure, the tangent at a point of a circle with centre and a diameter when extended intersect at . If , find .
In the adjoining figure, and are two tangents to a circle with centre from a point outside the circle. is a tangent to the circle at . Prove that, .
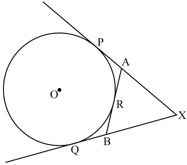
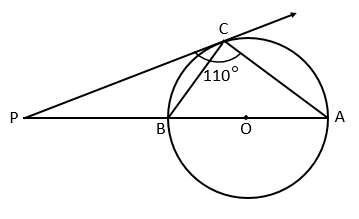
In the adjoining figure, and are tangents to the circle from an external point . is another tangent touching the circle at . If and , then find .
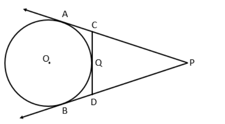
Let denotes the semi-perimeter of in which . If a circle touches the sides at respectively. Prove that .
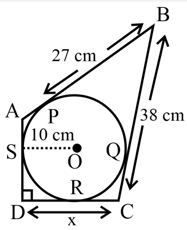
In the adjoining figure, quadrilateral is circumscribed. If the radius of incircle (centre ) is and . Find the value of .