Prove that the triangle formed by joining the mid-points of the sides of an equilateral triangle is also equilateral.

In $△\mathrm{ABC}, \mathrm{M}, \mathrm{N}$ and $\mathrm{P}$ are mid-points of sides $\mathrm{AB}, \mathrm{AC} \text{and} \mathrm{BC}$ respectively. $\mathrm{X},\hspace{0.17em}\mathrm{Y},\hspace{0.17em}\text{and} \mathrm{Z}$ are mid-points of sides of $△\mathrm{MNP}$. If $\mathrm{XY}=2.5 \mathrm{cm}, \mathrm{YZ}=3.5 \mathrm{cm} \text{and} \mathrm{XZ}=4 \mathrm{cm}$ and , find the sides of $△\mathrm{ABC}$.

$\mathrm{ABCD}$ is a parallelogram. $\mathrm{M}$ is the mid-point of $\mathrm{AB}$ and $\mathrm{P}$ is a point on diagonal $\mathrm{BD}$ such that $\mathrm{BP}=\frac{1}{4}\mathrm{BD}$. $\mathrm{MP}$ produced meets $\mathrm{BC}$ at $\mathrm{N}$. Prove that $\mathrm{N}$ is a mid-point of $\mathrm{BC}$.

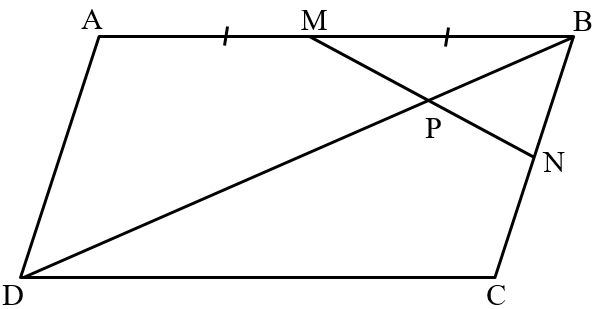
$\mathrm{ABCD}$ is a parallelogram. $\mathrm{M}$ is the mid-point of $\mathrm{AB}$ and $\mathrm{P}$ is a point on diagonal $\mathrm{BD}$ such that $\mathrm{BP}=\frac{1}{4}\mathrm{BD}$. $\mathrm{MP}$ produced meets $\mathrm{BC}$ at $\mathrm{N}$. $\mathrm{MN}=\frac{1}{2}\mathrm{AC}$

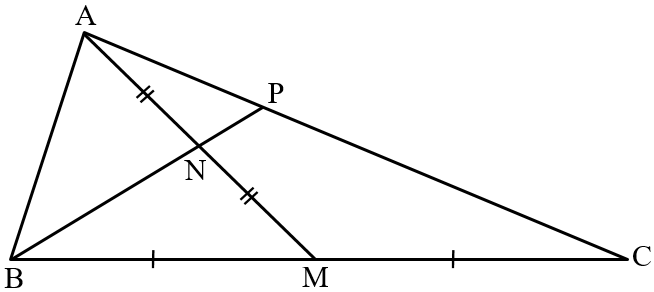
In $△\mathrm{ABC}, \mathrm{AM}$ is a median and $\mathrm{N}$ is the mid-points of $\mathrm{AM}$. $\mathrm{BN}$ produced meets $\mathrm{AC}$ at $\mathrm{P}$. Prove that $\mathrm{AP}=\frac{1}{3}\mathrm{AC}$.

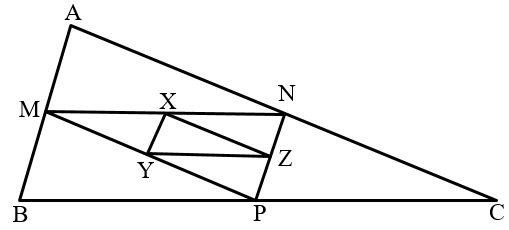
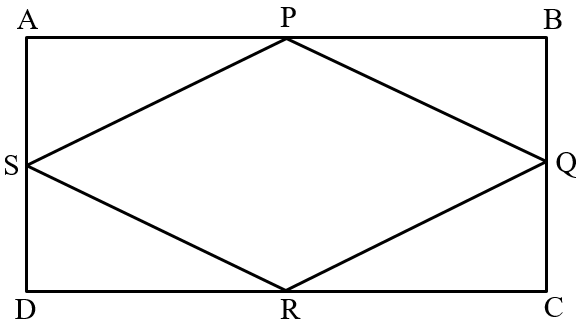
$\mathrm{ABCD}$ is a rectangle. $\mathrm{P},\mathrm{Q},\mathrm{R}$ and $\mathrm{S}$ are mid-points of sides of the rectangle as shown in the given figure. Prove that $\mathrm{PQRS}$ is a rhombus.

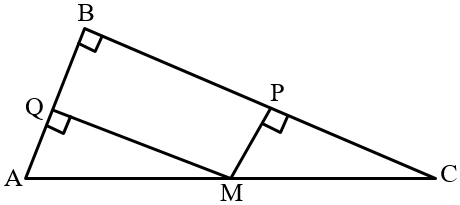
$\mathrm{ABC}$ is a right-angled triangle with hypotenuse $\mathrm{AC}=13 \mathrm{cm}$ and side $\mathrm{AB}=5 \mathrm{cm}$. Perpendiculars are drawn from mid-point $\mathrm{M}$ of $\mathrm{AC}$ to $\mathrm{AB}$ and $BC$. What is the perimeter of the resulting quadrilateral?

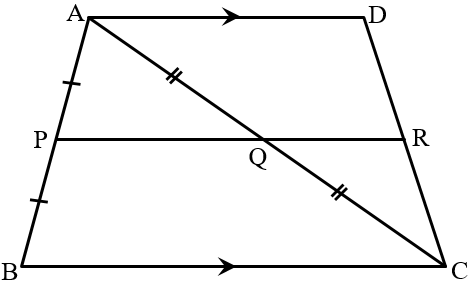
In the quadrilateral $\mathrm{ABCD}, \mathrm{AD}\parallel \mathrm{BC}. \mathrm{P}$ and $\mathrm{Q}$ are mid-points of $\mathrm{AB}$ and $\mathrm{AC}$. Prove that $\mathrm{R}$ is the mid-point of $\mathrm{DC}$.