Ramit is moving towards a stationary object of sound at a constant speed. At his initial position, he hears a pitch of $5$ hertz.

If the pitch from the source increases by $4$ hertz for every $5$ m Ramit travels, find the distance he would have travelled towards the source when the pitch is exactly $149$ hertz. Show your steps.

A stone is thrown into still water and the figure below represents the concentric circular phenomenon known as ripple effect. The radius of first circle is $3$ cm.

If the radius of each subsequent circle is $4$ cm more than the previous, which circle has a radius of $43$ cm? Show your steps.

$14,21,28,25,...$and $26,39,52,65,..$are two arithmetic progressions such that the $p$th term of the first arithmetic progression is the same as the $q$th term of the second arithmetic progression.

Derive a relationship between $p$ and $q$. Show your work.

Animation is a method in which a sequence of images are manipulated to appear as moving objects. An animation specialist wants to show the growth of a sapling into a tree through animation. She follows the steps below:

• She develops the first image by designing a sapling containing a certain number of leaves.
• She develops the second image by adding $15$ leaves to the first image.
• She develops the third image by adding $22$ leaves to the second image.
• She develops the fourth image by adding $29$ leaves to the third image and so on.

If she continues the process in the same manner, how many leaves will she be adding to the $25$th image to develop $26$th image? Show your work.

The sum of first two terms of an arithmetic progression is the same as the sum of the first seven terms of the same arithmetic progression.

Can such an arithmetic progression exist? Justify your answer,

Two arithmetic progressions have the same first term. The common difference of one progression is $4$ more than the other progression. $124$th term of the first arithmetic progression is same as $42$nd term of the second.

Find out set of possible values of the common differences. Show your work.

Sana decided to start practising for an upcoming marathon. She decided to gradually increase the duration. She ran for $10$ mins on day $1$ and increased the duration by $5$ minutes every day.

From which day onwards will she be running $2.5$ hours or more? Show your work.

Consider the list of numbers below.

$\frac{1}{2}+k, \frac{2}{3}+k, \frac{3}{4}+k, \frac{4}{5}+k,....$ where $k$ is an integer.

Is the above list of numbers an arithmetic progression? Justify your answer.

The exterior angles marked in each of the polygons below are in arithmetic progression.

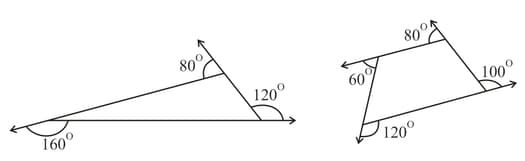
Minal drew one such polygon with $n$ sides. The smallest exterior angle is $8°$ and each subsequent angle is $4°$ more than previous angle.

Find the number of sides of the polygon that Minal had drawn. Show your steps.