A particle of mass M and positive charge Q , moving with a constant velocity u → 1 = 4 i ^ m s - 1 , enters a region of uniform static magnetic field normal to the x - y plane. The region of the magnetic field extends from x = 0 to x = L for all values of y . After passing through this region, the particle emerges on the other side after 10 milliseconds with a velocity u → 2 = 2 3 i ^ + j ^ m s - 1 . The correct statement (s) is (are)

The magnitude of the magnetic field 5 0 π M 3 Q units.

The direction of the magnetic field is +z direction.

The magnitude of the magnetic field 1 0 0 π M 3 Q units.

HARD

Earn 100

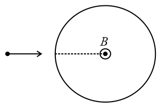
Several $\alpha$-particles of different speeds enter in a uniform magnetic field confined into a cylindrical region. If all the $α$ -particles enter the field radially, what can you say about time intervals spent by them in the magnetic field?

100% studentsanswered this correctly

Important Questions on Magnetic Effects of Current and Magnetism

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A proton and an alpha particle both enter a region of uniform magnetic field B, moving at right angles to the field B. if the radius of circular orbits for both the particles is equal and the kinetic energy acquired by proton is 1 MeV, the energy acquired by the alpha particle will be:

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

An electron, moving along the

x -

axis with an initial energy of

100 e V,

enters a region of magnetic field

\vec{B} = (1.5 \times 10^{- 3} T) \hat{k}

at S (see figure). The field extends between

x = 0

and

x = 2 c m .

The electron is detected at the point

Q

on a screen placed

8 c m

away from the point

S .

The distance d between

P

and

Q

(on the screen) is:
(electron’s charge

1.6 \times 10^{- 19} C

, mass of electron

= 9.1 \times 10^{- 31} k g

)

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A proton accelerated by a potential difference

500 kV

flies through a uniform transverse magnetic field

0.1 T

. The field is spread on a region of

1.0 cm

thickness. The angle through which the proton gets deviated from its original direction is (Proton mass

= 1.6 \times 10^{- 27} kg

and charge of proton

= 1.6 \times 10^{- 19} C

)

HARD

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

In the

xy - plane

, the region

y > 0

has a uniform magnetic field

B_{1} \hat{k}

and the region

y < 0

has another uniform magnetic field

B_{2} \hat{k}

. A positively charged particle is projected from the origin along the positive

y - axis

with speed

v_{0} = π m s^{- 1}

t = 0

, as shown in the figure. Neglect gravity in this problem. Let

t = T

be the time when the particle crosses the

x - axis

from below for the first time. If

B_{2} = 4 B_{1}

, the average speed of the particle, in

m s^{- 1}

, along the

x - axis

in the time interval

T

is ________.

Question Image

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

An electron is moving with a velocity

2 \times 10^{6} m / s

along positive

x

-direction in the uniform electric field of

8 \times 10^{7} V / m

applied along positive

y

-direction. The magnitude and direction of a uniform magnetic field (in tesla) that will cause the electrons to move undeviated along its original path is

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A proton of mass

m

moving with a speed

v

(< < c, velocity of light in vacuum)

completes a circular orbit in time

T

in a uniform magnetic field. If the speed of the proton is increased to

\sqrt{2} v

, what will be time needed to complete the circular orbit?

HARD

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

Two parallel metal plates $A$ and $B$ separated by a distance $25 cm$ are connected to an ammeter. Photons of energy $3.28 eV$ are incident on the photosensitive plate $A$ of threshold wavelength $5000 \overset{o}{A}$ . The minimum value of the magnetic field to be applied parallel to the plates so that the current through the ammeter becomes zero is $B \times 10^{- 5} T$ . Then the value of

$B$ is (mass of electron $= 9.0 \times 10^{- 31} kg$ , charge of electron $= 1.6 \times 10^{- 19} C$ )

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A deuteron and an alpha particle having equal kinetic energy enter perpendicular into a magnetic field. Let

r_{d}

and

r_{α}

be their respective radii of circular path. The value of

\frac{r_{d}}{r_{α}}

is equal to:

HARD

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A particle of mass

M

and positive charge

Q

, moving with a constant velocity

{\vec{u}}_{1} = 4 \hat{i} m s^{- 1}

, enters a region of uniform static magnetic field normal to the

x - y

plane. The region of the magnetic field extends from

x = 0

x = L

for all values of

y

. After passing through this region, the particle emerges on the other side after 10 milliseconds with a velocity

{\vec{u}}_{2} = 2 (\sqrt{3} \hat{i} + \hat{j}) m s^{- 1}

. The correct statement (s) is (are)

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii

r_{e}, r_{p}, r_{α}

respectively in a uniform magnetic field B. The relation between

r_{e}, r_{p}, r_{α}

is:

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

An electron having mass

9.1 \times 10^{- 31} kg,

charge

1.6 \times 10^{- 19} C

and moving with the velocity of

10^{6} m s^{- 1}

enters a region where magnetic field exists. If it describes a circle of radius

0.2 m

then intensity of magnetic field must be _____

\times 10^{- 5} T .

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A proton and an

α

- particle (with their masses in the ratio of

1 : 4

and charges in the ratio of

1 : 2

) are accelerated from rest through a potential difference

V .

If a uniform magnetic field

(B)

is set up perpendicular to their velocities, the ratio of the radii

r_{p} : r_{α}

of the circular paths described by them will be:

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A uniform magnetic field acts at a right angle to the direction of motion of a charged particle. As a result, the charged particle moves in a circular path of radius $2 cm$ . If both the charge and speed of the charged particles are made double, then the radius of the circular path will be

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

To which of the following quantities, the radius of the circular path of a charged particle moving at right angles to a uniform magnetic field is directly proportional?

HARD

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A charged particle of mass

m

and charge

q

with energy

E

enters a uniform transverse magnetic field

B

and describes a circular path. The magnitude of the angular momentum of the particle along the circular path is

L

. If the particle had energy

2 E

, the angular momentum would have been-

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

Two ions of masses $4 amu$ and $16 amu$ have charges $+ 2 e$ and $+ 3 e$ respectively. These ions pass through the region of the constant perpendicular magnetic field. The kinetic energy of both ions is the same. Then:

HARD

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

Two ions having same mass have charges in the ratio

1 : 2

. They are projected normally in a uniform magnetic field with their speeds in the ratio

2 : 3

. The ratio of the radii of their circular trajectories is,

EASY

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

Ionized hydrogen atoms and

α

-particles with same momenta enters perpendicular to a constant magnetic field

B

. The ratio of their radii of their paths

r_{H} : r_{α}

will be

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

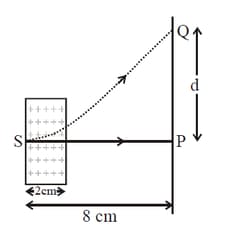
A rectangular region of dimensions $w \times I (w < < I)$ has a constant magnetic field into the plane of the paper as shown. On one side the region is bounded by a screen. On the other side positive ions of mass $m$ and charge $q$ are accelerated from rest and towards the screen by a parallel plate capacitor at constant potential difference $V < 0$ , and come out through a small hole in the upper plate. Which one of the following statements is correct regarding the charge on the ions that hit the screen?

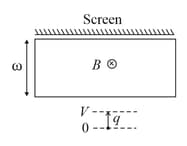
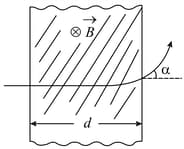
Question Image

MEDIUM

Physics>Electricity and Magnetism>Magnetic Effects of Current and Magnetism>Force on a Moving Charge

A proton (mass $m$ ) accelerated by a potential difference $V$ flies through a uniform transverse magnetic field $B$ . The field occupies a region of space by width $d$ . If $α$ be the angle of deviation of proton from the initial direction of motion (see figure), the value of $\sin α$ will be:
Question Image

Several $\alpha$-particles of different speeds enter in a uniform magnetic field confined into a cylindrical region. If all the α-particles enter the field radially, what can you say about time intervals spent by them in the magnetic field?

Important Questions on Magnetic Effects of Current and Magnetism

Learn and Prepare for any exam you want !

Several $\alpha$-particles of different speeds enter in a uniform magnetic field confined into a cylindrical region. If all the $α$ -particles enter the field radially, what can you say about time intervals spent by them in the magnetic field?