MEDIUM
9th CBSE
IMPORTANT
Earn 100
Show that a diagonal divides a parallelogram into two triangles of equal area.

Important Questions on Areas of Parallelograms and Triangles
MEDIUM
9th CBSE
IMPORTANT
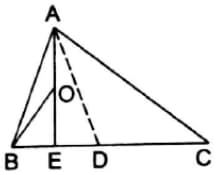
In the adjoining figure, and are two triangles on the same base . If line segment is bisected by at , show that
MEDIUM
9th CBSE
IMPORTANT
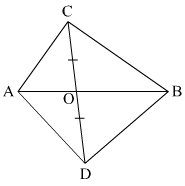
and are points on sides and respectively of such that Prove that
HARD
9th CBSE
IMPORTANT
is any point on the diagonalof a parallelogram. Prove that
MEDIUM
9th CBSE
IMPORTANT
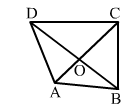
In the adjoining figure, the diagonals and of a quadrilateral intersect at
Ifprove that
MEDIUM
9th CBSE
IMPORTANT
The vertex of is joined to a point on the side . The midpoint of is .
Prove that

MEDIUM
9th CBSE
IMPORTANT
is the midpoint of side of and is the midpoint of . If is the midpoint of prove that
MEDIUM
9th CBSE
IMPORTANT
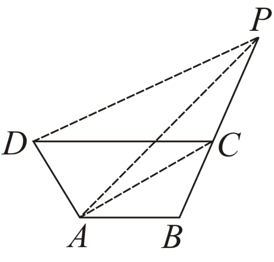
In a trapezium and is the midpoint of . Through , a line has been drawn which meets in and produced in as shown in the adjoining figure. Prove that
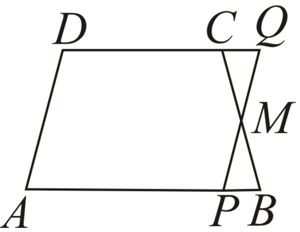
MEDIUM
9th CBSE
IMPORTANT
In the adjoining figure, is a quadrilateral. A line through, parallel to , meets produced in. Prove that