MEDIUM
Earn 100
Show that the median of a triangle divides it into two triangles of equal areas
Important Questions on Quadrilaterals
HARD
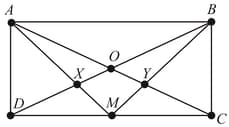
Let be a rectangle and be the midpoint of . Suppose and meet at and meet at , and meet at . Then
MEDIUM
MEDIUM
MEDIUM
MEDIUM
MEDIUM
EASY
Centroid of a triangle, whose vertices are is _____
EASY
MEDIUM
EASY
HARD
MEDIUM
MEDIUM
HARD
Let be the centroid of the triangle in which the angle is obtuse. Let and are the medians from and on the sides and respectively. If the four points and are concyclic, then
MEDIUM
HARD
EASY
HARD
HARD
HARD

