Shown below is a circle with multiple chords. One of the chords is the diameter of the circle.

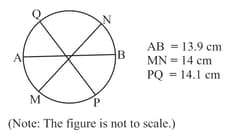
Find the measure of the angle subtended by a $4.7\pi \mathrm{cm}$ arc at the circumference of the circle. Show your work and give valid reasons.

Ramit drew two circles of different radii. Each of them had an arc that subtended an equal angle at the centre.

He said, "Both arcs are of the same length".
i) Is Ramit right?

ii) If both radii and angles subtended by the two arcs are different, can the arc lengths be the same?

A circle has radius 5 cm. Three chords of lengths 6 cm, 8 cm and 10 cm are drawn.

Which chord subtends the largest angle on its minor arc?

A cow is tied at one of the corners of a square shed. The length of the rope is 22 m. The cow can only eat the grass outside the shed as shown below.

What is the area that the cow can graze on? 

(Note: Give the answer in terms of $\mathrm{\pi }$)

Avikant bought a pair of glasses with wiper blades. He was curious to know the area being cleaned by each of the wiper blades. With the help of a ruler and a protractor, he found the length of each blade as 3 cm and the angle swept as 60°.

i) Find the area that each wiper cleans in one swipe, in terms of $\mathrm{\pi }$.
ii) If the diameter of each circular glass is 5 cm, what percent of the area of the glass will be cleaned by the blade in one swipe?

The figure below is a part of a circle with centre O. Its area is $\frac{1250\mathrm{\pi }}{9}{\mathrm{cm}}^2$ and the 10 sectors are identical.

Find the value of $\beta$ in degrees.

Shown below is a circle with centre O. Chord MN subtends an angle at centre O.

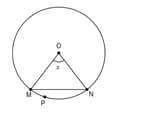
Which of these is true for the above circle?

$$\begin{gathered} 1. \frac{\mathrm{x}}{{360}^{\circ }}=\frac{\text{length of arc MPN}}{\text{circumference of the circle}} \\ 2. \frac{\mathrm{x}}{{360}^{\circ }}=\frac{\text{minor sector area}}{\text{area of the circle}} \end{gathered}$$

Shown below is a circle with centre O. The shaded sector has an angle of $280°$ and area $\mathrm{A} {\mathrm{cm}}^2$.

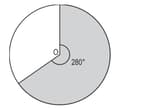
Which of these is the area of unshaded sector?

Raju and his $3$ friends ordered a pizza one night.

Now, the shop from where they bought this, did not cut it into equal pieces. Raju tried to divide it, but the pieces were not equal.  

As a fun game, he decided to measure the central angles formed and draw the pizza on a piece of paper.

He found that the radius of the pizza is $8 \mathrm{cm}$. The drawing of the pizza came out something like this:

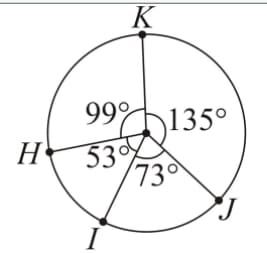
The area of the biggest share of pizza (correct to two decimal places) will be [assume $\mathrm{\pi }=\frac{22}{7}$]