Six identical cards are placed on a table. Each card has number $1$ marked on one side and number $2$ marked on its other side. All the six cards are placed such that the number $1$ is on the upper side. In one try, exactly four (neither more nor less) cards are turned upside down. In how many tries, can the cards be turned upside down such that all the six cards show number $2$ on the upper side?

Three persons A, B and C wore shirts of black, blue and orange colours (not necessarily in that order) and pants of green, yellow and orange colour (not necessarily in that order). No person wore a shirt and pant of the same colour. Further, it is given that

1. A did not wear shirt of black colour.

2. B did not wear shirt of blue colour.

3. C did not wear shirt of orange colour.

4. A did not wear pant of green colour.

5. B wore pant of orange colour.

What were the colours of the pant and shirt worn by C respectively?

In the figure shown below,

${\mathrm{S}}_1= \mathrm{a}+\mathrm{b}+\mathrm{c}, {\mathrm{S}}_2 = \mathrm{d}+\mathrm{e}+\mathrm{f}$

${\mathrm{S}}_3= \mathrm{g}+\mathrm{h}+\mathrm{i}, {\mathrm{S}}_4= \mathrm{a}+\mathrm{d}+\mathrm{g}$

${\mathrm{S}}_5= \mathrm{b}+\mathrm{e}+\mathrm{h}, {\mathrm{S}}_6 = \mathrm{c}+\mathrm{f}+\mathrm{i}$

$\mathrm{P} = \mathrm{a}\times \mathrm{e}\times \mathrm{i}$

If the numerical value of ${\mathrm{S}}_1, {\mathrm{S}}_2, {\mathrm{S}}_3, {\mathrm{S}}_4, {\mathrm{S}}_5, {\mathrm{S}}_6$  and $\mathrm{P}$ are known, what is the minimum number of values of the lowercase letters that must be given such that values of all the lowercase letters become known?

Seven players A, B, C, D, E, F, and G are to be seated such that,

1. B must always occupy the second position. 
2. F must always occupy the sixth position.
3. D and E must be seated adjacent to each other.

In how many different ways they can be seated?

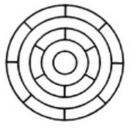
What is the minimum number of different colours required to paint the figure given below such that no two adjacent regions have the same colour?