State Ceva's theorem.
Important Questions on Theorems of Concurrency
In the given figure and if units then the value of will be
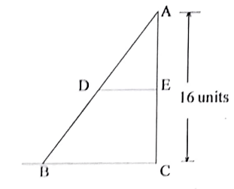
In If and If the length of , then find the value of .
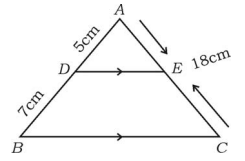
In and , find
In Fig 2, and . Prove that
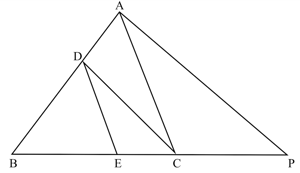
In a , a line parallel to intersects and at and . If , then is _____.
In trapezium ; The diagonals meet at . Prove that .
In the line parallel to meets and at and . If , then find .
Two parallel straight lines intersect three concurrent straight lines at and . Prove that .
In the line parallel to meets and at and and . If , then length of is
In the line parallel to meets and at and . If and , then what is the value of ?
In the line parallel to meets and at and . If then the length of is
In the line parallel to meets and at and . If and , thus what is the value of ?
In the line parallel to meets and at and . If then is equal to
In . If and , find the length of in centimrter.
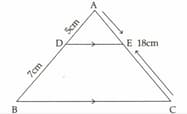
In the line parallel to meets and at and and . If , then length of is

