HARD
Earn 100
State and prove exterior angle theorem.
Important Questions on Angles
MEDIUM
HARD
is a quadrilateral in which . If , then is equal to
EASY
MEDIUM
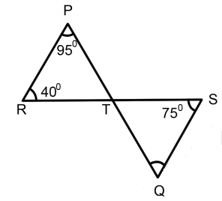
In the given figure, if line and the line intersect at such that , and and , then the value of will be
HARD
MEDIUM
HARD
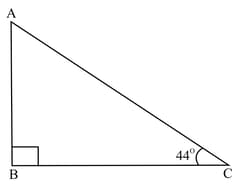
In the adjoining figure, is right-angled at . The point is on such that and is a parallelogram. If , then is equal to.
EASY
HARD
EASY
EASY
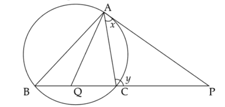
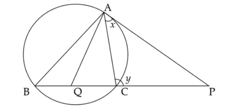
In the figure, chord is extended to . Tangent from to the circle is . is the bisector of . Prove that
HARD
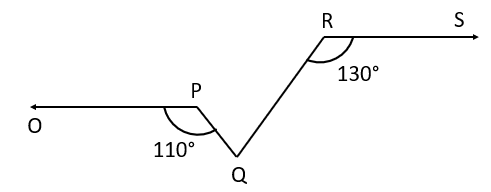
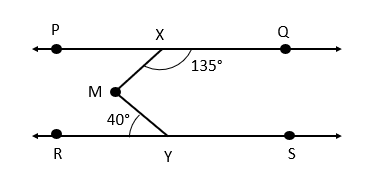
In the given figure, if , and , then the value of will be
MEDIUM
In the figure if and . Then the value of and will be
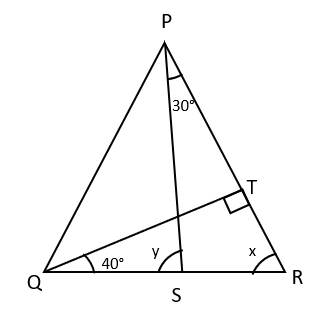
MEDIUM
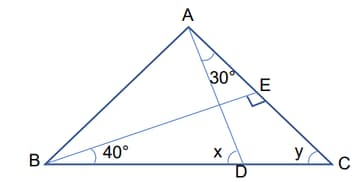
In the given figure, if , and , then the value of and are:
HARD
EASY
In the figure, chord is extended to . Tangent from to the circle is . is the bisector of . If and , then prove that .
MEDIUM