A particle of mass m is moving along the side of a square of side 'a', with a uniform speed υ in the x-y plane as shown in the figure: Which of the following statements is false for the angular momentum L → about the origin?

L → = m υ 2 R k ^ when the particle is moving from D to A.

L → = m υ R 2 + a k ^ when the particle is moving from B to C.

L → = - m υ 2 R k ^ when the particle is moving from A to B.

L → = m υ R 2 + a k ^ when the particle is moving from C to D.

HARD

Earn 100

State and prove principle of conservation of angular momentum. Explain it with examples.

Important Questions on Motion of System of Particles and Rigid Bodies

HARD

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A particle of mass m is moving along the side of a square of side 'a', with a uniform speed

\frac{d \vec{L}}{dt} = τ [\vec{r} \times \vec{F} = \vec{τ}]

in the x-y plane as shown in the figure:

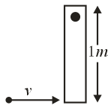
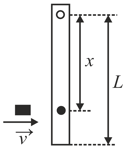
Question Image

Which of the following statements is false for the angular momentum

\vec{L}

about the origin?

HARD

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A disc of the moment of inertia

I_{1}

is rotating in a horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed

ω_{1}

Another disc of the moment of inertia

I_{2}

having zero angular speed is placed coaxially on a rotating disc. Now both the disc are rotating with the constant angular speed

ω_{2}

. The energy lost by the initial rotating disc is

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A ring of mass

M

and radius

R

is rotating with angular speed

ω

about a fixed vertical axis passing through its centre O with two point masses each of mass

\frac{M}{8}

at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is

\frac{8}{9} ω

and one of the masses is at a distance of

\frac{3}{5} R

from O. At this instant the distance of the other mass from O is

Question Image

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

Two coaxial discs, having moments of inertia

I_{1}

and

\frac{I_{1}}{2}

, are rotating with respective angular velocities

ω_{1}

and

\frac{ω_{1}}{2}

(in the same direction), about their common axis. They are brought in contact with each other and thereafter they rotate with a common angular velocity. If

E_{f}

and

E_{i}

are the final and initial total energies, then

(E_{f} - E_{i})

is:

HARD

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A hoop of radius

r

and mass

m

rotating with an angular velocity

ω_{0}

is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

The time dependence of the position of a particle of mass

m = 2

is given by

\vec{r} (t) = 2 t \hat{i} - 3 t^{2} \hat{j}

. Its angular momentum, with respect to the origin, at time

t = 2

is:

EASY

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A ball of mass

160 g

is thrown up at an angle of

60 °

to the horizontal at a speed of

10 m s^{- 1}

. The angular momentum of the ball at the highest point of the trajectory with respect to the point from which the ball is thrown is nearly

(g = 10 m s^{- 2})

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A thin rod of mass $0.9 kg$ and length $1 m$ is suspended, at rest, from one end so that it can freely oscillate in the vertical plane. A particle of mass $0.1 kg$ moving in a straight line with velocity $80 m s^{- 1}$ hits the rod at its bottom most point and sticks to it (see figure). The angular speed (in $rad s^{- 1}$ ) of the rod immediately after the collision will be …………

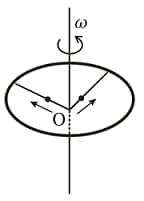
Question Image

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A particle of mass $2 kg$ is on a smooth horizontal table and moves in a circular path of radius $0.6 m$ . The height of the table from the ground is $0.8 m$ . If the angular speed of the particle is $12 rad s^{- 1}$ , the magnitude of its angular momentum about a point on the ground right under the center of the circle is:

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A bob of mass m attached to an inextensible string of length

l

is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed

ω

rad/s about the vertical. About the point of suspension :

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A thin smooth rod of length

L

and mass

M

is rotating freely with angular speed

ω_{0}

about an axis perpendicular to the rod and passing through center. Two beads of mass

m

and negligible size are at the center of the rod initially. The beads of mass

m

and negligible size are at the center of the rod initially. The beads are free to slide along the rod. The angular speed of the system, when the beads reach the opposite ends of the rod, will be:

HARD

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A particle of mass

20 g

is released with an initial velocity

5 m s^{- 1}

along the curve from the point

A,

as shown in the figure. The point

A

is at height

h

from point

B .

The particle slides along the frictionless surface. When the particle reaches point

B,

its angular momentum about

O

will be: (Take

g = 10 m s^{- 2}

)

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

Two uniform circular discs are rotating independently in the same direction around their common axis passing through their centres. The moment of inertia and angular velocity of the first disc are

0.1 kg - m^{2}

and

10 rad s^{- 1}

respectively while those for the second one are

0.2 kg - m^{2}

and

5 rad s^{- 1}

respectively. At some instant they get stuck together and start rotating as a single system about their common axis with some angular speed. The kinetic energy of the combined system is :

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A cubical block of side $30 cm$ is moving with velocity $2 m s^{- 1}$ on a smooth horizontal surface. The surface has a bump at a point $O$ as shown in the figure. The angular velocity (in rad/s) of the block immediately after it hits the bump, is :

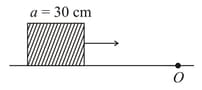
Question Image

EASY

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A person of

80 kg

mass is standing on the rim of a circular platform(disc like) of mass

200 kg

rotating about its axis at

5

revolutions per minute (rpm). The person now starts moving towards the centre of the platform. What will be the rotational speed (in

rpm

) of the platform when the person reaches its centre ?

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A rod of mass $m$ and length $L,$ pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed $v$ strikes the rod horizontally at a distance $x$ from its pivoted end and gets embedded in it. The combined system now rotates with an angular speed $ω$ about the pivot. The maximum angular speed $ω_{M}$ is achieved for $x = x_{M}$ . Then

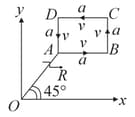
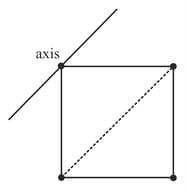
Question Image

MEDIUM

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

Four point masses, each of mass $m$ , are fixed at the corners of a square of side I. The square is rotating with angular frequency $ω,$ about an axis passing through one of the corners of the square and parallel to the diagonal, as shown in the figure. The angular momentum of the square about the axis is

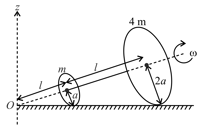
Question Image

EASY

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

Two rotating bodies,

A

and

B

of masses,

m

and

2 m

with moments of inertia

I_{A}

and

I_{B} (I_{B} > I_{A})

have equal kinetic energy of rotation. If,

L_{A}

and

L_{B}

be their angular momenta, respectively, then,

EASY

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

A force

\vec{F} = α \hat{i} + 3 \hat{j} + 6 \hat{k}

is acting at a point

\vec{r} = 2 \hat{i} - 6 \hat{j} - 12 \hat{k}

. The value of

α

for which angular momentum about origin is conserved is:

HARD

Physics>Mechanics>Motion of System of Particles and Rigid Bodies>Angular Momentum

Two thin circular discs of mass $m$ and $4 m$ , having radii of $a$ and $2 a$ , respectively, are rigidly fixed by a massless, right rod of length $l = \sqrt{24} a$ through their center. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $ω$ . The angular momentum of the entire assembly about the point $O$ is $\vec{L}$ (see the figure). Which of the following statement(s) is(are) true?

Question Image

State and prove principle of conservation of angular momentum. Explain it with examples.

Important Questions on Motion of System of Particles and Rigid Bodies

Learn and Prepare for any exam you want !