EASY

Earn 100

Suppose R is the region bounded by the two curves $y = x^{2}$ and $y = 2 x^{2} - 1$ as shown in the following diagram

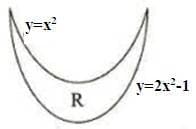
Two distinct lines are drawn such that each of these lines partitions the regions into at least two parts. If 'n' is the total number of regions generated by these lines, then

50% studentsanswered this correctly

Important Questions on Geometry

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

The value of

p

, for which the points

A (3, 1)

B (5, p)

and

C (7, - 5)

are collinear is

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

What is the area (in square units) of the triangular region enclosed by the graphs of the equations

x + y = 3, 2 x + 5 y = 12

and the

x

-axis?

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

P (8, 10)

and

Q (14, - 2)

are two given points and the point

R

divides the line-segment

P Q

externally in the ratio

8 : 6

. The coordinates of

R

are

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

A straight line through the origin

O

meets the parallel lines

4 x + 2 y = 9

and

2 x + y + 6 = 0

P

and

Q

respectively. The point

O

divides the segment

P Q

in the ratio

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

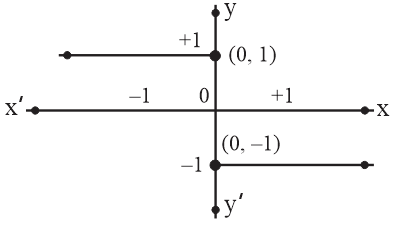
The equation of the graph shown here is:

Question Image

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

P (- 3, - 2, 4), Q (- 9, - 8, 10)

and

R (- 5, - 4, 6)

are collinear, then the ratio in which

R

divides

P Q

HARD

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Let

S

be the focus of parabola

x^{2} + 8 y = 0

and

Q

be any point on it. If

P

divides the line segment

S Q

in the ratio

1 : 2,

then the locus of

P

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

The equation of the straight line passing through the point

M (- 5, 4)

, such that the portion of it between the axes is divided by the point

M

in to two equal halves, is

HARD

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

If the distance between the points

(x, 0)

and

(- 7, 0)

10

. Then, the possible values of

x

are ______.

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

In the given figure, $A P$ bisect $∠ B A C$ . If $AB = 4 cm, AC = 6 cm$ and $BP = 3 cm$ , then the length of $CP$ is:

Question Image

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Let

x_{0}, y_{0}

be fixed real numbers such that

x_{0}^{2} + y_{0}^{2} > 1

. If

x, y

are arbitrary real numbers such that

x^{2} + y^{2} \leq 1,

then the minimum value of

{(x - x_{0})}^{2} + {(y - y_{0})}^{2}

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Find the ratio in which line $3 x + 2 y = 17$ divides the line segment joined by points $(2, 5)$ and $(5, 2) .$

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

The ratio in which the straight line

3 x + 4 y = 6

divides the join of the points

(2, - 1)

and

(1, 1)

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Find the area of

∆ A B C

Whose vertices are

A (10, - 6), B (2, 5)

and

C (- 1, 3) .

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

The centre of a circle is

(- 6, 4)

. If one end of the diameter of the circle is at

(- 12, 8)

then the other end is at:

HARD

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

If $A (0, - 1), B (2, 1)$ and $C (0, 3)$ are the vertices of $△ A B C$ , then the length of median drawn from $A$ will be

HARD

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Quadrilateral formed by the vertices

(1, 4), (- 5, 4), (- 5, - 3)

and

(1, - 3)

will be

EASY

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

△ ABC, D, E

and

F

are the midpoints of the sides AB, BC and CA, respectively. If

AB = 12 cm, BC = 20 cm

and

CA = 15 cm

, then the value of

\frac{1}{2} (DE + EF + DF)

is:

HARD

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Find the area of the triangle formed by the lines

x - 3 y = 0, x - y = 4

and

x + y = 4 .

MEDIUM

Quantitative Aptitude>Geometry>Geometry>Geometrical Shapes

Find the area of the triangle formed with the three straight lines represented by:

$(i) x + y = 0 (i i) 3 x = 5 y; a n d (i i i) y = 3 x - 12$

Suppose R is the region bounded by the two curves y=x2 andy=2x2-1 as shown in the following diagram Two distinct lines are drawn such that each of these lines partitions the regions into at least two parts. If 'n' is the total number of regions generated by these lines, then

Important Questions on Geometry

Learn and Prepare for any exam you want !

Suppose R is the region bounded by the two curves $y = x^{2}$ and $y = 2 x^{2} - 1$ as shown in the following diagram

Two distinct lines are drawn such that each of these lines partitions the regions into at least two parts. If 'n' is the total number of regions generated by these lines, then