The Jupiter's period of revolution around the Sun is times that of the Earth. Assuming the planetary orbits to be circular, find,
how many times the distance between the Jupiter and the Sun exceeds that between the Earth and the Sun,
the velocity and the acceleration of Jupiter in the heliocentric reference frame.
Take (, Radius of Jupiter's orbit = )

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS
Find the potential energy of the gravitational interaction
(a) of two mass points of masses and located at a distance from each other;
(b) of a mass point of mass and a thin uniform rod of mass and length if they are located along a straight line, at a distance from each other. Also, find the force of their interaction.
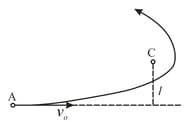
A cosmic body moves towards the Sun with velocity (when far from the Sun) and aiming parameter , the arm of the vector , relative to the centre of the Sun. Find the minimum distance by which this body will get to the Sun.
A particle of mass is located outside a uniform sphere of mass , at a distance from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.
