The angular momentum of a particle relative to a certain point $O$ varies with time as $\overrightarrow{M}=\overrightarrow{a}+\overrightarrow{b}{t}^2$, where $\overrightarrow{a}$ and $\overrightarrow{b}$ are constant vectors, with $\overrightarrow{a}\perp \overrightarrow{b}$. Find the force moment $\overrightarrow{N}$ relative to the point $O$ acting on the particle when the angle between the vectors $\overrightarrow{N}$ and $\overrightarrow{\mathit{M}}$ equals $45°$.

A plank of mass $m_1$, with a uniform sphere of mass $m_2$ placed on it, rests on a smooth horizontal plane. A constant horizontal force $F$ is applied to the plank. With what accelerations will the plank and the centre of the sphere move, provide there is no sliding between the plank and the sphere?

In the arrangement shown in the figure, weight $A$ possesses mass $m$, a pulley $B$ possesses mass $M$. Also known are the moment of inertia$I$ of the pulley relative to its axis and the radii of the pulley are $R$ and $2R$, respectively. Consider the mass of the threads is negligible. Find the acceleration of weight $A$ after the system is set free. (Assume no slipping takes place anywhere and axis of cylinder remains horizontal)

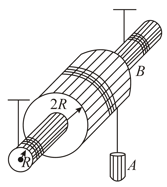
A window (of weight $w$) is supported by two strings passing over two smooth pulleys in the frame of the window in which window just fits in, the other ends of the string being attached to weights each equal to half the weight of the window. One thread breaks and the window moves down. Find acceleration of the window if $\mu$ is the coefficient of friction, and $a$ is the height and $b$ the breadth of the window.

A $160 \mathrm{mm}$ diameter pipe of mass $6 \mathrm{kg}$ rests on a $1.5 \mathrm{kg}$ plate. The pipe and plate are initially at rest when a force $P$ of magnitude $25 \mathrm{N}$ is applied for $0.75 \mathrm{s}$. Knowing that ${\mathrm{\mu }}_{\mathrm{s}}=0.25 \mathrm{and} {\mathrm{\mu }}_{\mathrm{k}}=0.20$ between the plate and both the pipe and the floor, determine;

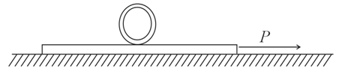
(a) whether the pipe slides with respect to the plate.

(b) the resulting velocities of the pipe and of the plate.

A uniform disc of mass $m$ and radius $R$ is projected horizontally with velocity $v_0$ on a rough horizontal floor, so that it starts off with a purely sliding motion at $t = 0$. After $t_0$seconds, it acquires a purely rolling motion as shown in the figure.

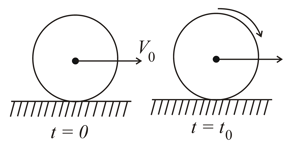
(a) Calculate the velocity of the centre of mass of the disc at $t_0$.

(b) Assuming the coefficient of friction to be $\mu$, calculate $t_0$. Also calculate the work done by the frictional force as a function of time and  the total work done by it over a time $t$ much longer than $t_0$.

Two uniform thin rods $A\mathit{ }\mathrm{and}\mathit{ }B$ of length $0.6 \mathrm{m}$ each and of masses $0.01 \mathrm{kg} \mathrm{and} 0.02 \mathrm{kg}$, respectively, are rigidly joined, end to end. The combination is pivoted at the lighter end $P$ as shown in figure such that it can freely rotate about the point $P$ in a vertical plane. A small object of mass $0.05 \mathrm{kg}$ moving horizontally hits the lower end of the combination and sticks to it. What should be the velocity of the object so that the system could just be raised to the horizontal position?

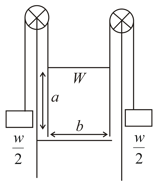
A bar of mass $m$ is held as shown between $4$ disks, each of mass $M \mathrm{and} \mathrm{radius} r=75 \mathrm{mm}$. Determine the acceleration of the bar immediately after it has been released from rest, knowing that the normal forces exerted on the disks are sufficient to prevent any slipping and assuming that; In (i) case, the discs are attached to the fixed support on wall. In (ii) case, the discs are attached to the bar.

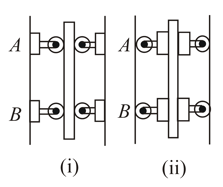
(a) $m=5 \mathrm{kg} \mathrm{and} M=2 \mathrm{kg}$.

(b) the mass of $M$ of the disks is negligible.

(c) the mass of $m$ of the bar is negligible.