The area of the circle circumscribing three circles of unit radius touching each other is

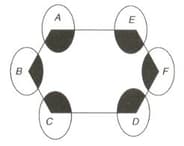
Find the sum of the areas of the shaded sectors given that $ABCDFE$ is any hexagon and all the circles are of same radius $r$ with different vertices of the hexagon as their centres as shown in the figure.

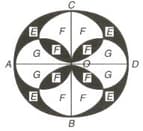
ABCD is a circle and circles are drawn with AO,CO, DO and OB as diameters.Areas E and F are shaded. E/F is equal to

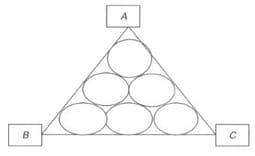
The diagram shows six equal circles inscribed in equilateral triangle $ABC$. The circles touch externally among themselves and also touch the sides of the triangle. If the radius of each circle is $R$, area of the triangle is

A boy Mithilesh was playing with a square cardboard of side $2$ meters. While playing, he accidentally sliced off the corners of the cardboard in such a manner that a figure having all its sides equal was generated. The area of this eight-sided figure is:

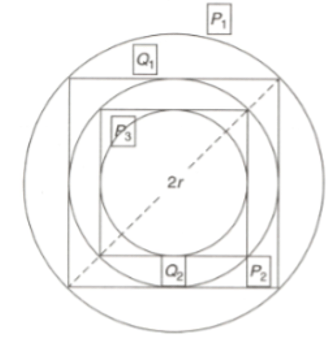
Let $P_1$ be the circle of radius $r$. $A$ square $Q_1$ is inscribed in $P_1$ such that all the vertices of the square $Q_1$ lie on the circumference of $P_1$. Another square $Q_2$ is inscribed in the circle $P_2$. Circle $P_3$ is inscribed in the square $Q_2$ and so on. If $S_N$ is the area between $Q_N$ and $P_{N-1}$ where $N$ represents the set of natural numbers. If the ratio of sum of all such $S_N$ to that of the area of the square $Q_1$ is $\frac{a-\mathrm{\pi }}{b}$ then $a+b=$?