HARD

Earn 100

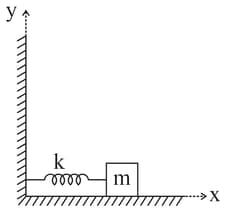
The centre of a solid sphere of mass $m$ and radius $R$ placed on a rough horizontal plane is connected to a spring of stiffness $k$ as shown. An impulse is provided to the sphere at its mean position and the sphere starts oscillating. Find the period of oscillation, if there is no slipping anywhere

50% studentsanswered this correctly

Important Questions on Oscillations

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

The total energy of a body executing simple harmonic motion is

E

. The kinetic energy when the displacement is

1 / 3

of the amplitude

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A body of mass $1 kg$ is executing simple harmonic motion. Its displacement $y (cm)$ at $t$ seconds is given by $y = 6 \sin (100 t + \frac{π}{4})$ . Its maximum kinetic energy is

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

The physical quantity conserved in simple harmonic motion is

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

In the following sentence, a blank space with four options is given. Select whichever preposition or determiner you consider the most appropriate for the blank space.

These are the good rules to live _____.

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

Two sentences are given below and you are required to find the correct sentence which combines both the sentences.

Which is the correct combination of the given two sentences?

He is too tired. He could not stand.

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

Total energy of a particle performing S.H.M. is NOT proportional to

HARD

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A potential is given by

V (x) = \frac{k (x + a)^{2}}{2}

for

x < 0

and

V (x) = \frac{k (x - a)^{2}}{2}

for

x > 0

. The schematic variation of oscillation period

T

for a particle performing periodic motion in this potential as a function of its energy

E

is:

HARD

Physics>Oscillations and Waves>Oscillations>Energy in SHM

An object of mass

0.5 kg

is executing simple harmonic motion. It amplitude is

5 cm

and time period (T) is

0.2 s

. What will be the potential energy of the object at an instant

t = \frac{T}{4} s

starting from mean position. Assume that the initial phase of the oscillation is zero.

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

Directions: Each of the following sentences in this section has a blank space and four words or group of words given after the sentence. Select the word or group of words you consider most appropriate for the blank space and indicate your response on the Answer Sheet accordingly.

Every rash driver becomes a ____ killer.

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A simple pendulum of length

L

has mass

M

and it oscillates freely with amplitude

A

. At the extreme position, its potential energy is (

g

= acceleration due to gravity)

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

For what value of displacement the kinetic energy and potential energy of a simple harmonic oscillation become equal?

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A particle is executing simple harmonic motion

(S H M)

of amplitude

A,

along the

x

-axis, about

x = 0 .

When its potential Energy

(P E)

equals kinetic energy

(K E),

the position of the particle will be:

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

An object of mass $4 kg$ is attached to a spring which is fixed at one end on a rigid support and the mass-spring system is kept on a frictionless table. The object is allowed to execute simple harmonic motion along $X$ - direction. The force constant of the spring is $10 N m^{- 1}$ and the spring is stretched initially a distance of $5 cm$ , the total energy stored in the system is

Question Image

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A body is executing S.H.M. Its potential energy is

E_{1}

and

E_{2}

at displacements

x

and

y

respectively. The potential energy at displacement

(x + y)

HARD

Physics>Oscillations and Waves>Oscillations>Energy in SHM

In a simple harmonic oscillation, what fraction of total mechanical energy is in the form of kinetic energy, when the particle is midway between mean and extreme position.

EASY

Physics>Oscillations and Waves>Oscillations>Energy in SHM

Total energy of a particle of mass '

m

' executing SHM given by

y = A \sin ω t

for any displacement is:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A particle starts executing simple harmonic motion

(SHM)

of amplitude

a

and total energy

E .

At any instant, its kinetic energy is

\frac{3 E}{4}

, then its displacement

y

is given by:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

The maximum value attained by the tension in the string of a swinging pendulum is four times the minimum value it attains. There is no slack in the string. The angular amplitude of the pendulum is

MEDIUM

Physics>Oscillations and Waves>Oscillations>Energy in SHM

A particle is executing simple harmonic motion with a time period

T

. At time

t = 0

, it is at its position of equilibrium. The kinetic energy - time graph of the particle will look like:

HARD

Physics>Oscillations and Waves>Oscillations>Energy in SHM

For a simple pendulum, a graph is plotted between its kinetic energy (K.E.) and potential energy (P.E.) against its displacement d. which one of the following represents these correctly? (graphs are schematic and not drawn to scale)

The centre of a solid sphere of mass m and radius R placed on a rough horizontal plane is connected to a spring of stiffness k as shown. An impulse is provided to the sphere at its mean position and the sphere starts oscillating. Find the period of oscillation, if there is no slipping anywhere

Important Questions on Oscillations

Learn and Prepare for any exam you want !