EASY

Earn 100

The circular motion of a particle with constant speed is

50% studentsanswered this correctly

Important Questions on Simple Harmonic Motion

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

If the differential equation for a simple harmonic motion is

\frac{d^{2} y}{d t^{2}} + 2 y = 0

, the time period of the motion is,

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.
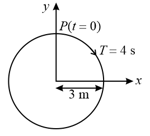
Question Image

y

-projection of the radius vector of rotating particle

P

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A body of mass $1 kg$ is executing simple harmonic motion. Its displacement $y (cm)$ at $t$ seconds is given by $y = 6 \sin (100 t + \frac{π}{4})$ . Its maximum kinetic energy is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle of mass

0.1 kg

is executing simple harmonic motion of amplitude

0.1 m

. When the particle passes through the mean position, its kinetic energy is

8 \times 10^{- 3} J

. If the initial phase is

45 °,

the equation of its motion is (Assume,

x (t)

as the position of the particle at time

t

)

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle is executing a simple harmonic motion. Its maximum acceleration is

α

and maximum velocity is

β

. Then, its time period of vibration will be:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A simple pendulum oscillates harmonically about

x = 0

with an amplitude

A

and time period

T

. Its speed at

x = A / 2

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

The oscillation of a body on a smooth horizontal surface is represented by the equation,

X = A \cos (ω t)

, where

X =

displacement at time

t

ω =

frequency of oscillation,

a =

acceleration at time

t

and

T =

time period.
Which one of the following graph shows correctly the variation

a

with

t

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

In the case of a simple pendulum executing

SHM,

t = 0

, the bob is not at the mean position. The graph drawn between the tension

(T)

in the string and time

(t)

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A simple pendulum of length

L

has mass

M

and it oscillates freely with amplitude

A

. At the extreme position, its potential energy is (

g

= acceleration due to gravity)

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

Which of the following equation represents a simple harmonic motion? (

ω

is angular frequency, A is amplitude of oscillation and

i = \sqrt{- 1}

)

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle is executing SHM along a straight line. Its velocities at distances

x_{1}

and

x_{2}

from the mean position are

V_{1}

and

V_{2}

respectively. Its time period is:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle performs

S . H . M .

with amplitude

A

. Its speed is tripled at the instant when it is at a distance of

\frac{2 A}{3}

from the mean position. The new amplitude of the motion is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

x, v

and

a

denote the displacement, the velocity and the acceleration of a particle executing

S H M

of time period

T

. Then, which of the following does not change with time?

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A mass

M

is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes

S . H . M .

of period

T

. If the mass is increased by

m

, the time period becomes

\frac{5 T}{3} .

What is the ratio

(\frac{M}{m})

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

Y = A \sin (ω t + ϕ_{0})

is the time-displacement equation of a

S H M .

t = 0

the displacement of the particle is

Y = \frac{A}{2}

and it is moving along negative

x

-direction. Then the initial phase angle

ϕ_{0}

will be:

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

The physical quantity conserved in simple harmonic motion is

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A body is in simple harmonic motion with time period

T = 0.5 s

and amplitude

A = 1 cm

. Find the average velocity in the interval in which it moves from equilibrium position to half of its amplitude.

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

A particle is performing SHM starting from extreme position. Graphical representation shows that, between displacement and acceleration, there is a phase difference of

EASY

Physics>Oscillations and Waves>Simple Harmonic Motion>Simple Harmonic Motion

Which of the following plots represents schematically the dependence of the time period of a pendulum if measured and plotted as a function of its oscillations? (Note: amplitude need not be small)

The circular motion of a particle with constant speed is

Important Questions on Simple Harmonic Motion

Learn and Prepare for any exam you want !