The cost of designing an aircraft, per kilogram, at time years after can be modelled as a continuous variable. The rate of increase of is directly proportional to . Write down a differential equation that is satisfied by . In , the cost of designing an aircraft was per kilogram. After years, the cost of designing an aircraft was per kilogram. Find the cost of designing an aircraft after years.

Important Questions on Differential Equations
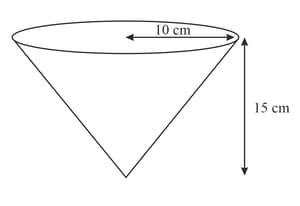
The diagram shows an inverted cone filled with liquid paint. An artist cuts a small hole in the bottom of the cone and the liquid paint drips out at a rate of per second. At time seconds after the hole is cut, the paint in the cone is an inverted cone of depth
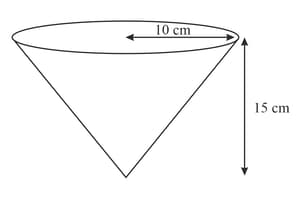
Show that
The diagram shows an inverted cone filled with liquid paint. An artist cuts a small hole in the bottom of the cone and the liquid paint drips out at a rate of per second. At time seconds after the hole is cut, the paint in the cone is an inverted cone of depth
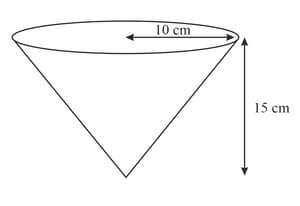
The diagram shows an inverted cone filled with liquid paint. An artist cuts a small hole in the bottom of the cone and the liquid paint drips out at a rate of per second. At time seconds after the hole is cut, the paint in the cone is an inverted cone of depth
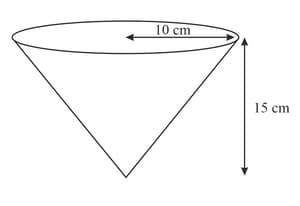
The diagram shows an inverted cone filled with liquid paint. An artist cuts a small hole in the bottom of the cone and the liquid paint drips out at a rate of per second. At time seconds after the hole is cut, the paint in the cone is an inverted cone of depth