MEDIUM
NEET
IMPORTANT
Earn 100
The dependence of acceleration due to gravity on the distance from the centre of the earth, assumed to be a sphere of radius of uniform density is as shown in figures below. The correct figure is.
(a)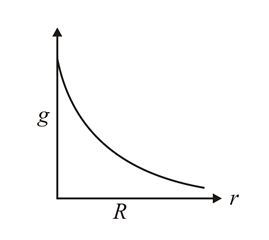

(b)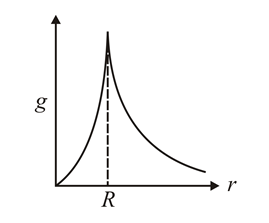

(c)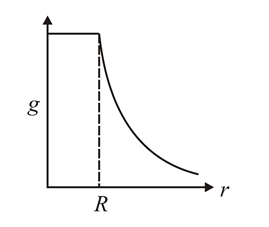

(d)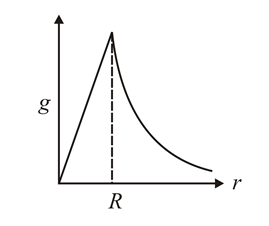

66.67% studentsanswered this correctly

Important Questions on Gravitation
EASY
NEET
IMPORTANT
MEDIUM
NEET
IMPORTANT
EASY
NEET
IMPORTANT
EASY
NEET
IMPORTANT
Which one of the following plots represents the variation of the gravitational field on a particle with distance due to a thin spherical shell of radius ? ( is measured from the centre of the spherical shell)
MEDIUM
NEET
IMPORTANT
EASY
NEET
IMPORTANT
EASY
NEET
IMPORTANT
MEDIUM
NEET
IMPORTANT
