The diagram shows a shaded region, bounded by the curves and . The area of the region can be written in the form . Find the values of .
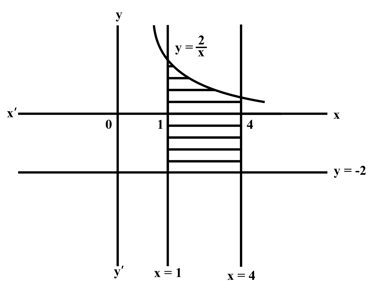


Important Questions on From Approximation to Generalization: Integration
Consider the functions . Part of the graphs of are shown in the diagram. Find the coordinates of the points of intersection of the graphs of .
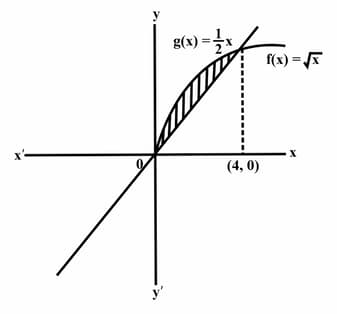
Consider the functions . Part of the graphs of are shown in the diagram. Write an integral expression for the area enclosed by the graph of .
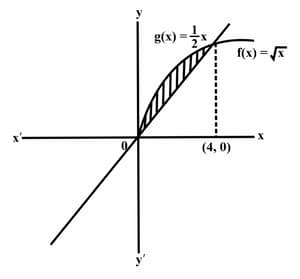
Consider the functions . Part of the graphs of are shown in the diagram. Find the shaded region area.
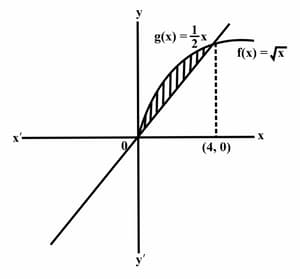
Consider the functions . Part of the graphs of are shown in the diagram. The line divides the area of the region in half. Write down an integral expression for half the area of the region.
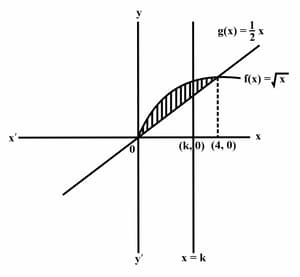
Consider the functions . Part of the graphs of are shown in the diagram. The line divides the area of the region in half. Find an expression, not involving an integral, for half the area of the region.
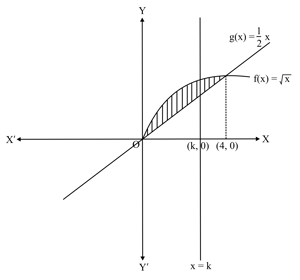
Consider the functions . Part of the graphs of are shown in the diagram. The line divides the area of the region in half. Using your GDC, find the value of .
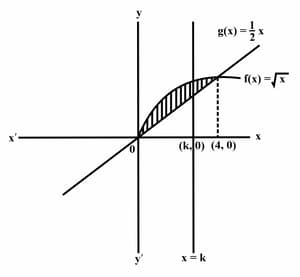
Write an integral expression to find the area of the region bounded by the two curves , and then find this area. Use your GDC to examine the graphs and evaluate any definite integrals.
Write an integral expression to find the area of the region bounded by the two curves , and then find this area. Use your GDC to examine the graphs and evaluate any definite integrals.
