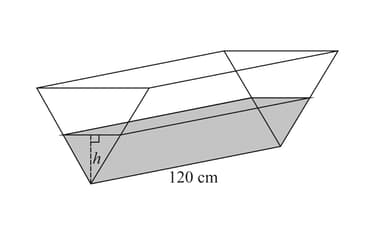
The diagram shows a water container in the shape of a triangular prism of length cm.The vertical cross-section is an equilateral triangle. Water is poured into the container at a rate of . Show that the volume of water in the container, , is given by , where cm is the height of the water in the container.


Important Questions on Further Differentiation
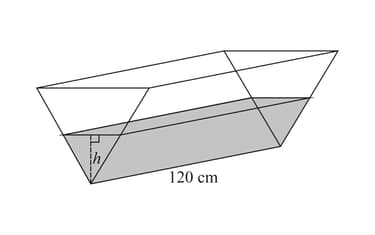
The diagram shows a water container in the shape of a triangular prism of length cm.The vertical cross-section is an equilateral triangle. Water is poured into the container at a rate of . Find the rate of change of when cm.
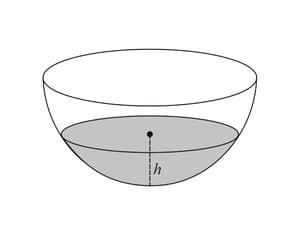
Water is poured into the hemispherical bowl of radius cm at a rate of . After seconds, the volume of water in the bowl, is given by , where cm is the height of the water in the bowl. Find the rate of change of when cm.
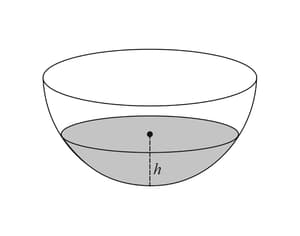
Water is poured into the hemispherical bowl of radius cm at a rate of . After seconds, the volume of water in the bowl, is given by , where cm is the height of the water in the bowl. Find the rate of change of when cm.
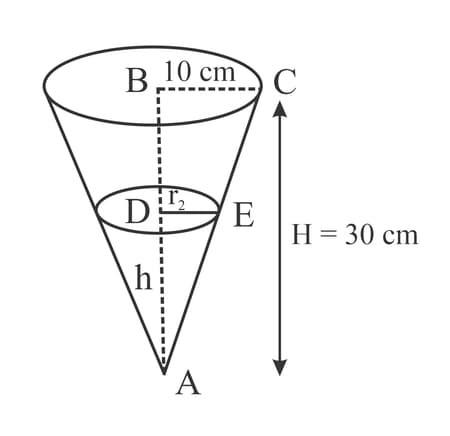
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Show that the volume of water in the cone, , when the height of the water is cm is given by the formula .
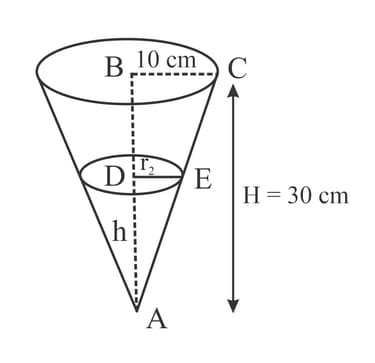
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Find the rate of change of , when cm.
Oil is poured onto a flat surface and a circular patch is formed. The radius of the patch increases at a rate of . Find the rate at which the area is increasing when the circumference is .
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the radius of the patch after seconds.
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the rate of increase of the radius of the patch after seconds.
